Giải SBT Toán 7 Bài 16. Định lí và chứng minh định lí có đáp án

Viết giả thiết và kết luận bằng kí hiệu:

Chứng minh định lí:

Theo GT ta có:

• $\widehat{A}$ bù với $\widehat{C}$ nên $\widehat{A}+\widehat{C}=180°$

Suy ra $\widehat{A}=180°-\widehat{C}$        (1)

• $\widehat{B}$ bù với $\widehat{C}$ nên $\widehat{B}+\widehat{C}=180°$

Suy ra $\widehat{B}=180°-\widehat{C}$         (2)

Từ (1) và (2) suy ra $\widehat{A}=\widehat{B}.$

Vậy $\widehat{A}=\widehat{B}.$

a) Hình vẽ minh họa:

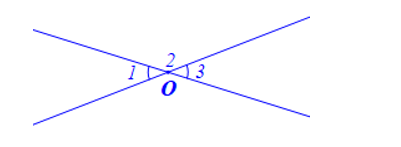
Viết giả thiết và kết luận bằng kí hiệu:

Hình vẽ minh họa:

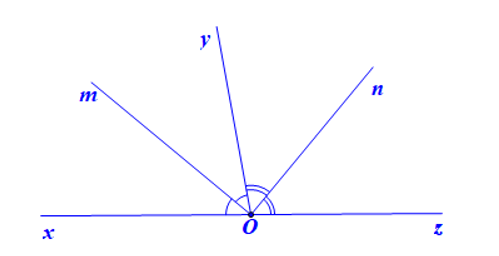
Viết giả thiết và kết luận bằng kí hiệu:

Chứng minh định lí:

Vì tia Om là tia phân giác của $\widehat{xOy}$ nên ta có:

$\widehat{xOm}=\widehat{mOy}=\frac{1}{2}\widehat{xOy}$      (1)

Vì tia On là tia phân giác của $\widehat{zOy}$ nên ta có:

$\widehat{yOn}=\widehat{nOz}=\frac{1}{2}\widehat{yOz}$         (2)

Từ (1) và (2) ta có:

$\widehat{mOy}+\widehat{yOn}=\frac{1}{2}\widehat{xOy}+\frac{1}{2}\widehat{yOz}$$=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)$

Mà $\widehat{xOy}$ và $\widehat{yOz}$ là hai góc kề bù nên:

$\widehat{xOy}+\widehat{yOz}=180°$

Do đó $\widehat{mOy}+\widehat{yOn}=\frac{1}{2}.180°=90°$

Hay $\widehat{mOn}=90°.$

Vậy $\widehat{mOn}=90°.$

Hình vẽ minh họa:

Viết giả thiết và kết luận bằng kí hiệu:

Chứng minh định lí:

Vì a ⊥ c (GT) nên ${\widehat{A}}_1=90°$

Vì b ⊥ c (GT) nên ${\widehat{B}}_1=90°$

Do đó ${\widehat{A}}_1={\widehat{B}}_1=90°$

Mà hai góc ${\widehat{A}}_1$ và ${\widehat{B}}_1$ ở vị trí đồng vị

Suy ra a // b.

Vậy a // b.

a) Hai góc cùng phụ một góc thứ ba thì bằng nhau.