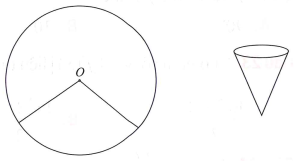
Bác Bính có một tấm thép mỏng hình tròn tâm O bán kính 4dm. Bác định cắt ra một hình quạt tròn tâm O, quấn rồi hàn ghép hai mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (Bỏ qua phần mối hàn và độ dày của tấm thép)

Quảng cáo
Trả lời:
Đáp án D
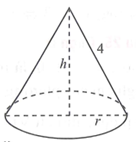
Gọi bán kính đáy hình nón là r.
Ta có: với .
Xét hàm trên có:
Bảng biến thiên:
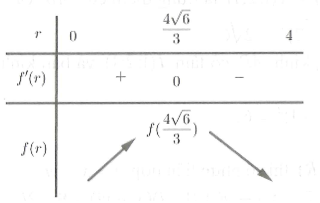
Từ bảng biến thiên ta thấy, hàm số f(r) đạt GTLN khi .
Vậy .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D
Đồ thị hàm số có đường tiệm cận đứng là .
Đồ thị hàm số có đường TCĐ là .
Câu 2
B. 20
Lời giải
Đáp án A
TXĐ: Ta có: .
Để hàm số đã cho nghịch biến trên (1;2) thì và bằng 0 tại hữu hạn điểm.
Hàm số đồng biến trên nên cũng đồng biến trên (1;2).
Lại có và nên .
Vậy có 11 giá trị của m.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.