Câu hỏi:
16/06/2022 3,561
Tổng số điểm mà các thành viên đội tuyển Olympic Toán quốc tế (IMO) của Việt Nam đạt được trong 20 kì thi được cho ở bảng sau:
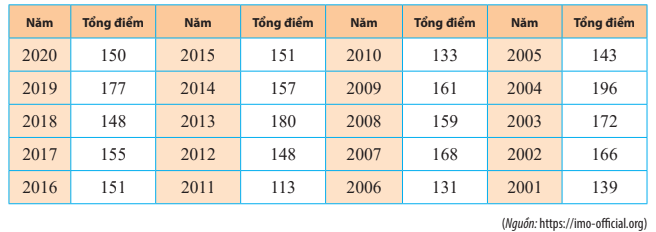
Có ý kiến cho rằng điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020. Hãy sử dụng số trung bình và trung vị để kiểm nghiệm xem ý kiến trên có đúng không?
Tổng số điểm mà các thành viên đội tuyển Olympic Toán quốc tế (IMO) của Việt Nam đạt được trong 20 kì thi được cho ở bảng sau:
Có ý kiến cho rằng điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020. Hãy sử dụng số trung bình và trung vị để kiểm nghiệm xem ý kiến trên có đúng không?
Quảng cáo
Trả lời:
Giải bởi Vietjack
+ Trong giai đoạn từ năm 2001 đến năm 2010:
Cỡ mẫu là n1 = 10.
Số trung bình:
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
131; 133; 139; 143; 159; 161; 166; 168; 172; 196.
Vì cỡ mẫu là số chẵn nên số trung vị là .
+ Trong giai đoạn từ năm 2011 đến năm 2020:
Cỡ mẫu là n2 = 10.
Số trung bình:
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
113; 148; 148; 150; 151; 151; 155; 157; 177; 180.
Vì cỡ mẫu là số chẵn nên số trung vị là .
+ Nếu dựa theo số trung bình, ta có: 156,8 > 153 nên điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020.
+ Nếu dựa theo số trung vị, ta có: 160 > 151 nên điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020.
Vậy dựa vào cả số trung vị và số trung bình, ta thấy rằng ý kiến đã cho đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Cỡ mẫu là n = 1 + 3 + 5 + 2 + 1 = 12.
Số trung bình là: .
Số thí sinh là trong thời gian 7 phút là nhiều nhất nên mốt của mẫu là Mo = 7.
Sắp xếp các giá trị của mẫu theo thứ tự không giảm, ta được:
5; 6; 6; 6; 7; 7; 7; 7; 7; 8; 8; 35.
Vì cỡ mẫu là số chẵn nên tứ phân vị thứ hai là Q2 = .
Tứ phân vị thứ nhất là trung vị của mẫu: 5; 6; 6; 6; 7; 7. Do đó Q1 = 6.
Tứ phân vị thứ ba là trung vị của mẫu: 7; 7; 7; 8; 8; 35. Do đó Q3 = 7,5.
b) Dựa theo số trung bình, vì 9,08 > 7 nên thời gian thi của các thí sinh năm nay nhiều hơn năm ngoái.
Dựa theo trung vị, thì cả hai năm trung vị đều bằng nhau và bằng 7 nên thời gian của các thí sinh trong hai năm là ngang nhau.
Vì trong mẫu số liệu của năm nay có số liệu 35 lớn hơn so với các số liệu còn lại rất nhiều, do đó ta dùng trung vị để so sánh sẽ phù hợp hơn.
Vậy thời gian thi nói chung của các thí sinh trong hai năm là ngang nhau.
Lời giải
a) Bảng số liệu là bảng tần số.
Cỡ mẫu là n = 6 + 8 + 10 + 6 + 4 + 3 = 37.
Số trung bình của mẫu là:
.
Giá trị 28 có tần số lớn nhất nên mốt của mẫu là Mo = 28.
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
23; 23; 23; 23; 23; 23; 25; 25; 25; 25; 25; 25; 25; 25; 28; 28; 28; 28; 28; 28; 28; 28; 28; 28; 31; 31; 31; 31; 31; 31; 33; 33; 33; 33; 37; 37; 37.
Vì cỡ mẫu là số lẻ nên tứ phân vị thứ hai là Q2 = 28.
Tứ phân vị thứ nhất là trung vị của mẫu: 23; 23; 23; 23; 23; 23; 25; 25; 25; 25; 25; 25; 25; 25; 28; 28; 28; 28. Do đó Q1 = 25.
Tứ phân vị thứ ba là trung vị của mẫu: 28; 28; 28; 28; 28; 31; 31; 31; 31; 31; 31; 33; 33; 33; 33; 37; 37; 37. Do đó Q3 = 31.
b) Bảng số liệu là bảng tần số tương đối.
Số trung bình là: .
Tần số tương đối là tỉ số của tần số với cỡ mẫu, do đó, giá trị có tần số tương đối lớn nhất thì có tần số lớn nhất, vậy giá trị 0 có tần số lớn nhất nên mốt của mẫu số liệu là Mo = 0.
Giả sử cỡ mẫu là n = 10, khi đó:
Tần số của giá trị 0 là 0,6 . 10 = 6.
Tần số của giá trị 2 là 0,2 . 10 = 2.
Tần số của giá trị 4 là 0,1 . 10 = 1.
Tần số của giá trị 5 là 0,1 . 10 = 1.
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
0; 0; 0; 0; 0; 0; 2; 2; 4; 5.
Vì cỡ mẫu là số chẵn nên tứ phân vị thứ hai là Q2 = 0.
Tứ phân vị thứ nhất là trung vị của mẫu: 0; 0; 0; 0; 0. Do đó Q1 = 0.
Tứ phân vị thứ ba là trung vị của mẫu: 0; 2; 2; 4; 5. Do đó Q3 = 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)