Câu hỏi:

13/07/2024 3,721

Cho hình thoi ABCD có góc A bằng 60 độ , kẻ BH vuông góc với AD tại H . Gọi O là giao điểm của AC và BD; E là điểm đối xứng của B qua H; F là điểm đối xứng của C qua B.

a) Tứ giác ABCD là hình gì? Vì sao?

b) Chứng minh tứ giác ABCE là hình thang cân.

c)
Kẻ $A K ⊥ O E$ tại K. Gọi L là trung điểm của đoạn EK. Chứng minh AL//FK.

Xem lời giải

Câu hỏi trong đề: Bộ đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

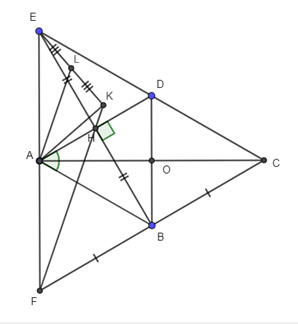
Cho hình thoi ABCD có góc A bằng 60 độ , kẻ BH vuông góc với AD tại H . Gọi O là giao điểm của AC và BD; E là điểm đối xứng của B qua H; F là điểm đối xứng của C qua B. a) Tứ giác ABCD là hình gì? Vì sao? b) Chứng minh tứ giác ABCE là hình thang cân. (ảnh 1)

a) Xét tam giác ABD có AB = AD (do ABCD là hình thoi)

Suy ra tam giác ABD cân

Mà $\hat{B A D} = 60^{0}$ nên tam giác ABD đều

Ta lại có BH là đường cao nên BH cũng là đường trung tuyến của

tam giác ABD.

suy ra H là trung điểm của AD.

Xét tứ giác ABDE có hai đường chéo AD và BE cắt nhau tại H

H là trung điểm của BE (do B và E đối xứng với nhau qua H)

H là trung điểm của AD (cmt)

Do đó ABDE là hình bình hành

Mà $A D ⊥ B E$ tại H (gt).

suy ra ABDE là hình thoi.

b. Ta có DE//AB (ABDE là hình thoi) và DC//AB (ABCD là hình thoi) nên ED, DC trùng nhau

suy ra E,D,C thẳng hàng

Xét tứ giác ABCE có AB // DE nên tứ giác ABCE là hình thang (1)

Ta có: $\hat{B A D} = \hat{B C D} = 60^{0}$ (hai góc đối trong hình thoi ABCD)

Do tam giác ABD đều nên AB = BD = AD = AE = DE

Suy ra tam giác AED đều

$\Rightarrow \hat{A E D} = 60^{0}$

$\Rightarrow \hat{A E D} = \hat{B C D} (= 60 °)$ (2)

Từ (1) và (2) suy ra ABCE là hình thang cân.

c. Vì ABCD là hình thoi có hai đường chéo AC giao BD tại O nên O là trung điểm của AC

Xét tam giác ACF có:

O là trung điểm của AC (cmt)

B là trung điểm của CF (C và F đối xứng với nhau qua B)

Suy ra OB là đường trung bình của tam giác ACF.

suy ra OB // AF

Mà BD // AE (ABDE là hình thoi)

Do đó AF trùng với AE hay A, F, E thẳng hàng.

Xét tam giác CFE, có :

D là trung điểm của CE

AD // EF

Suy ra A là trung điểm của EF.

Xét tam giác KFE, có :

L là trung điểm của KE (gt)

A là trung điểm của EF (cmt)

Suy ra AL là đường trung bình của tam giác FKE.

Suy ra AL//FK

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm tất cả các tam giác vuông có số đo các cạnh là các số nguyên dương và số đo diện tích bằng số đo chu vi.

Xem đáp án

Lời giải

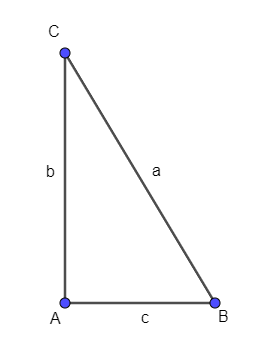
Tìm tất cả các tam giác vuông có số đo các cạnh là các số nguyên dương và số đo diện tích bằng số đo chu vi. (ảnh 1)

Khi đó, ta có: a, b, c là các số nguyên dương và $1 \leq b \leq c < a$ .

Diện tích tam giác ABC là: $S_{A B C} = \frac{1}{2} b c$ .

Chu vi tam giác ABC là: a + b + c.

Theo đầu bài, ta có: $a + b + c = \frac{1}{2} b c$

$\Leftrightarrow 2 (a + b + c) = b c$ (*)

Do tam giác ABC vuông tại A nên ta có: $a^{2} = b^{2} + c^{2}$ (định lý Py – ta – go)

$\Leftrightarrow a^{2} = {(b + c)}^{2} - 2 b c$

$\Leftrightarrow a^{2} = {(b + c)}^{2} - 4 (a + b + c)$

$\Leftrightarrow a^{2} = {(b + c)}^{2} - 4 a - 4 (b + c)$

$\Leftrightarrow a^{2} + 4 a = {(b + c)}^{2} - 4 (b + c)$

$\Leftrightarrow a^{2} + 4 a + 4 = {(b + c)}^{2} - 4 (b + c) + 4$

$\Leftrightarrow {(a + 2)}^{2} = {(b + c - 2)}^{2}$

$\Leftrightarrow a + 2 = b + c - 2 (b + c \geq 2)$

$\Leftrightarrow a = b + c - 4$

Thay a = b + c – 4 vào (*) ta được:

2(b + c – 4 + b + c) = bc

$\Leftrightarrow$ 4b + 4c – 8 – bc = 0

$\Leftrightarrow$ (4b – bc) + (4c – 16) = - 8

$\Leftrightarrow$ b(4 – c) + 4(c – 4) = - 8

$\Leftrightarrow$ (b – 4)(4 – c) = - 8

$\Leftrightarrow$ (b – 4)(c – 4) = 8

Vì b, c là các số nguyên dương nên ta có các trường hợp sau:

TH1: ${\begin{cases} b - 4 = 4 \\ c - 4 = 2 \end{cases} \Leftrightarrow {\begin{cases} b = 8 \\ c = 6 \end{cases} \Rightarrow a^{2} = 8^{2} + 6^{2} = 100 \Leftrightarrow a = 10.$

TH2: ${\begin{cases} b - 4 = 1 \\ c - 4 = 8 \end{cases} \Leftrightarrow {\begin{cases} b = 5 \\ c = 12 \end{cases} \Rightarrow a^{2} = 5^{2} + 12^{2} = 169 \Leftrightarrow a = 13.$

Vậy có hai tam giác vuông thỏa mãn yêu cầu bài toán là hai tam giác có các kích thước là: (6, 8, 10) và (5, 12, 13).

Câu 2

Cho $x + 2 y = 5$ . Tính giá trị của biểu thức

$A = x^{2} + 4 y^{2} - 2 x + 10 + 4 xy - 4 y$

Xem đáp án

Lời giải

Ta có: $A = x^{2} + 4 y^{2} - 2 x + 10 + 4 xy - 4 y$

= (x² + 4xy + 4y²) + (-2x – 4y) + 10

= (x + 2y)² – 2(x + 2y) + 10

Thay x + 2y = 5 vào biểu thức A, ta có:

A= 5² – 2.5 + 10 = 25 – 10 + 10 = 25.

Vậy với x + 2y = 5 thì A = 25.

Câu 3

Tìm đa thức thương và đa thức dư trong phép chia sau:

(2x³ – 7x² + 13x + 2) : (2x – 1).

b) Xác định số hữu tỉ a để f(x) = x³ – 2x² + 5x + a chia hết cho đa thức g(x) = x – 3.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho $A = \frac{2 x + 1}{(x - 4) (x - 3)} - \frac{x + 3}{x - 4} + \frac{2 x + 1}{x - 3} .$

a) Rút gọn biểu thức A.

b) Tính giá trị của biểu thức A biết x² = 9.

c) Tìm giá trị nhỏ nhất của B biết B = A.(x² – 5x + 4).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Phân tích đa thức thành nhân tử:

a. $x^{2} - 4 y^{2} - 2 x + 4 y$

b. $(x^{2} + 2 x) (x^{2} + 2 x - 2) - 3$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Tìm tất cả các tam giác vuông có số đo các cạnh là các số nguyên dương và số đo diện tích bằng số đo chu vi.

Cho x+2y=5. Tính giá trị của biểu thức A=x2+4y2−2x+10+4xy−4y

Tìm đa thức thương và đa thức dư trong phép chia sau: (2x3 – 7x2 + 13x + 2) : (2x – 1). b) Xác định số hữu tỉ a để f(x) = x3 – 2x2 + 5x + a chia hết cho đa thức g(x) = x – 3.

Cho A=2x+1(x−4)(x−3)−x+3x−4+2x+1x−3. a) Rút gọn biểu thức A. b) Tính giá trị của biểu thức A biết x2 = 9. c) Tìm giá trị nhỏ nhất của B biết B = A.(x2 – 5x + 4).

Phân tích đa thức thành nhân tử: a. x2−4y2−2x+4y b. (x2+2x)(x2+2x−2)−3

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho $x + 2 y = 5$ . Tính giá trị của biểu thức

$A = x^{2} + 4 y^{2} - 2 x + 10 + 4 xy - 4 y$

Tìm đa thức thương và đa thức dư trong phép chia sau:

(2x³ – 7x² + 13x + 2) : (2x – 1).

b) Xác định số hữu tỉ a để f(x) = x³ – 2x² + 5x + a chia hết cho đa thức g(x) = x – 3.

Cho $A = \frac{2 x + 1}{(x - 4) (x - 3)} - \frac{x + 3}{x - 4} + \frac{2 x + 1}{x - 3} .$

a) Rút gọn biểu thức A.

b) Tính giá trị của biểu thức A biết x² = 9.

c) Tìm giá trị nhỏ nhất của B biết B = A.(x² – 5x + 4).

Phân tích đa thức thành nhân tử:

a. $x^{2} - 4 y^{2} - 2 x + 4 y$

b. $(x^{2} + 2 x) (x^{2} + 2 x - 2) - 3$