Câu hỏi:

13/07/2024 1,009

a. Nêu tính chất đường trung bình của tam giác?

b. Cho tam giác ABC. Gọi M là trung điểm của AB, N là trung điểm của AC, biết BC = 10cm. Tính MN.

Xem lời giải

Câu hỏi trong đề: Bộ đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a. Nêu đúng tính chất ĐTB của tam giác như SGK

Đường trung bình của một tam giác song song với cạnh đáy và bằng một nửa cạnh đáy.

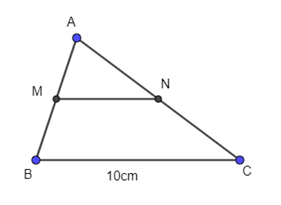
- Xét tam giác ABC, có:

M là trung điểm của AB

N là trung điểm của AC

Suy ra MN là đường trung bình của tam giác ABC.

Do đó MN =

\frac{B C}{2} = \frac{10}{2}

= 5cm

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho ABC vuông tại A (AB < AC). Gọi I là trung điểm BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.

a. Tứ giác AMIN là hình gì? Vì sao?

b. Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi.

c. Đường thẳng BN cắt DC tại K. Chứng minh $\frac{D K}{D C} = \frac{1}{3}$

Xem đáp án

Lời giải

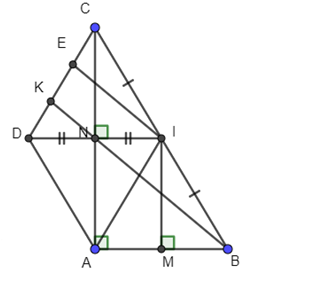
Cho ABC vuông tại A (AB < AC). Gọi I là trung điểm BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N. a. Tứ giác AMIN là hình gì? Vì sao? b. Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi. c. Đường thẳng BN cắt DC tại K. Chứng minh DK/DC=1/3 . (ảnh 1)

a. Chứng minh đúng ANIM là hình chữ nhật có 3 góc vuông:

Xét tứ giác ANIM có:

$\hat{B A C} = \hat{I M A} = \hat{I N A} = 90^{0} .$

Suy ra tứ giác ANIM là hình chữ nhật.

b. - Giải thích được IN vừa là đường cao vừa là trung tuyến của tam giác AIC:

Xét $Δ A I C$ , có: AI = $\frac{1}{2} B C = I B = I C$ (tính chất đường trung tuyến trong tam giác vuông ABC)

$\Rightarrow Δ A I C$ cân tại I

Mà $I N ⊥ A C$ hay IN là đường cao

$\Rightarrow$ IN là đường trung tuyến

$\Rightarrow$ N là trung điểm của AC.

- Chứng minh ADCI là hình bình hành có hai đường chéo vuông góc:

Xét tứ giác ADCI, có:

Hai đường chéo AC và AI cắt nhau tại N.

Mà N là trung điểm của AC, N là trung điểm của DI.

Suy ra tứ giác ADCI là hình bình hành.

Mặt khác $A C ⊥ D I$ tại N

Do đó tứ giác ADCI là hình thoi.

c. - Kẻ thêm đường thẳng qua I song song với BK cắt CD tại E và chứng minh được EK = EC:

Kẻ đường thẳng qua I song song với BK cắt CD tại E.

Xét $Δ B K C$ , có:

I là trung điểm của BC (gt)

IE // BK

Suy ra E là trung điểm của KC hay EC = EK (1).

- Chứng minh được EK = DK:

Xét $Δ D I E$ , có:

N là trung điểm của DI (gt)

NK // IE (BK // IE)

Suy ra K là trung điểm của DE hay DK = KE (2)

- Từ (1) và (2) Suy ra

\frac{D K}{D C} = \frac{1}{3}

Câu 2

Phân tích các đa thức sau thành nhân tử.

a. 3a + 3b – a² – ab

b. x² + x + y² – y – 2xy

c. - x² + 7x – 6

Xem đáp án

Lời giải

a. - Nhóm đúng (3a +3b) – (a² + ab)

- Đặt nhân tử chung đúng 3(a + b) – a(a + b)

- Đúng kết quả (a + b)(3 – a)

b. - Nhóm đúng (x² – 2xy + y²) + (x – y)

- Dùng đúng H ĐT (x – y)² + (x – y)

- Đúng kết quả (x – y)(x – y + 1)

c. - Tách đúng – (x² – x – 6x + 6)

= - [x(x – 1) – 6(x – 1)]

= - (x – 1)(x – 6)

Câu 3

Thực hiện phép tính.
a. $\frac{6 x z - 7 x^{2}}{4 y^{2}} + \frac{9 y z + 7 x^{2}}{4 y^{2}}$

b. $(\frac{2 x}{2 x + y} - \frac{4 x^{2}}{4 x^{2} + 4 x y + y^{2}}) : (\frac{2 x}{4 x^{2} - y^{2}} + \frac{1}{y - 2 x})$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho phân thức A = $\frac{3 x^{3} + 6 x^{2}}{x^{3} + 2 x^{2} + x + 2}$

a/ Tìm điều kiện của x để giá trị của phân thức xác định.

b/ Tìm giá trị của x để phân thức có giá trị bằng 2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

a. Nêu tính chất đường trung bình của tam giác? b. Cho tam giác ABC. Gọi M là trung điểm của AB, N là trung điểm của AC, biết BC = 10cm. Tính MN.

Phân tích các đa thức sau thành nhân tử. a. 3a + 3b – a2 – ab b. x2 + x + y2 – y – 2xy c. - x2 + 7x – 6

Thực hiện phép tính. a. 6xz−7x24y2+9yz+7x24y2 b. (2x2x+y−4x24x2+4xy+y2):(2x4x2−y2+1y−2x)

Cho phân thức A = 3x3+6x2x3+2x2+x+2 a/ Tìm điều kiện của x để giá trị của phân thức xác định. b/ Tìm giá trị của x để phân thức có giá trị bằng 2.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

a. Nêu tính chất đường trung bình của tam giác?

b. Cho tam giác ABC. Gọi M là trung điểm của AB, N là trung điểm của AC, biết BC = 10cm. Tính MN.

Phân tích các đa thức sau thành nhân tử.

a. 3a + 3b – a² – ab

b. x² + x + y² – y – 2xy

c. - x² + 7x – 6

Thực hiện phép tính.
a. $\frac{6 x z - 7 x^{2}}{4 y^{2}} + \frac{9 y z + 7 x^{2}}{4 y^{2}}$

b. $(\frac{2 x}{2 x + y} - \frac{4 x^{2}}{4 x^{2} + 4 x y + y^{2}}) : (\frac{2 x}{4 x^{2} - y^{2}} + \frac{1}{y - 2 x})$

Cho phân thức A = $\frac{3 x^{3} + 6 x^{2}}{x^{3} + 2 x^{2} + x + 2}$

a/ Tìm điều kiện của x để giá trị của phân thức xác định.

b/ Tìm giá trị của x để phân thức có giá trị bằng 2.