Câu hỏi trong đề: Đề kiểm tra giữa kì 2 Toán 8 có đáp án ( Mới nhất) !!
Quảng cáo
Trả lời:
Đáp án A và C
- Xét phương trình (x2 + 1)(x + 2) = 0.
Thay x = −2 vào biểu thức (x2 + 1)(x + 2), ta được:
[(−2)2 + 1].(−2 + 2) = [(−2)2 + 1].0 = 0.
Do đó x = −2 là nghiệm của phương trình (x2 + 1)(x + 2) = 0.
- Xét phương trình .
ĐKXĐ: x ≠ ± 2
Ta thấy x = −2 (không TM ĐKXĐ) nên x = −2 không phải là nghiệm của phương trình .
- Xét phương trình 2x2 + 7x + 6 = 0.
Thay x = −2 vào biểu thức 2x2 + 7x + 6, ta được:
2.(−2)2 + 7.(−2) + 6 = 8 −14 + 6 = −6 + 6 = 0.
Do đó x = −2 là nghiệm của phương trình 2x2 + 7x + 6 = 0.
- Xét phương trình
ĐKXĐ: x ≠ −2.
Ta thấy x = −2 (không TM ĐKXĐ) nên x = −2 không phải là nghiệm của phương trình .
Từ đó suy ra: x = −2 là nghiệm của các phương trình (x2 + 1)(x + 2) = 0 và 2x2 + 7x + 6 = 0.
Vậy chọn A và C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải


a) Vì ABCD là hình chữ nhật nên AB // CD.
Suy ra (hai góc so le trong).
Xét DAHB và DBCD có:
(chứng minh trên)
Do đó ∆AHB ![]() ∆BCD (g.g).
∆BCD (g.g).
b) Từ câu a: ∆AHB![]() ∆BCD suy ra: (1)
∆BCD suy ra: (1)
Lại có CE là đường phân giác trong ∆BCD nên (2)
Từ (1) và (2) suy ra .
Do đó AH.ED = HB.EB (đpcm)
c) Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta được:
AB2 + AD2 = BC2
.
Ta có
Khi đó
.
Áp dụng định lý Py-ta-go vào ∆ADH vuông tại H, ta được:
AH2 + DH2 = AD2
.
Do đó, EH = ED – DH = .
Mặt khác, từ câu a: ∆AHB ![]() ∆BCD suy ra:
∆BCD suy ra:
.
Do đó
Vậy diện tích tứ giác AECH là 10,15 cm2.
Lời giải
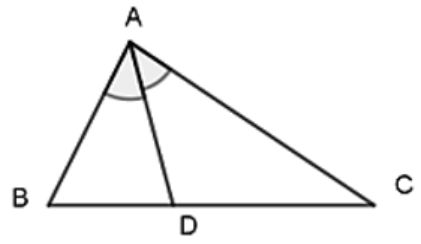
Trong ∆ABC có AD là phân giác của góc BAC.
Áp dụng tính chất đường phân giác của tam giác, ta được: .
.
Vậy chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.