Câu hỏi:

19/08/2025 490

Cho đồ thị của hàm số $y = (m - \frac{1}{2}) x$ (với m là hằng số, $m \neq \frac{1}{2})$ đi qua điểm A (2; 6).

a) Xác định m.

b) Vẽ đồ thị của hàm số đã cho với giá trị m tìm được ở câu a. Tìm trên đồ thị hàm số trên điểm có tung độ bằng 2.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Hàm số $y = (m - \frac{1}{2}) x$ (với m là hằng số, $m \neq \frac{1}{2})$ đi qua điểm A (2; 6).

Nên: $6 = (m - \frac{1}{2}) . 2$

$m - \frac{1}{2} = 3$

$m = \frac{7}{2}$ .

Vậy $m = \frac{7}{2}$ .

b) Với $m = \frac{7}{2}$ , ta có đồ thị hàm số y = 3x.

* Cách vẽ:

- Vẽ hệ trục tọa độ Oxy.

- Đồ thị hàm số đi qua O (0; 0).

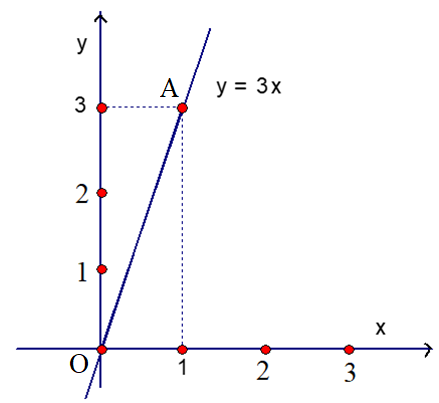
- Với x = 1 ta được y = 1. 3 = 3, điểm A (1; 3) thuộc đồ thị hàm số y = 3x.

Do đó, đường thẳng OA là đồ thị của hàm số đã cho.

* Ta có đồ thị hàm số y = 3x.

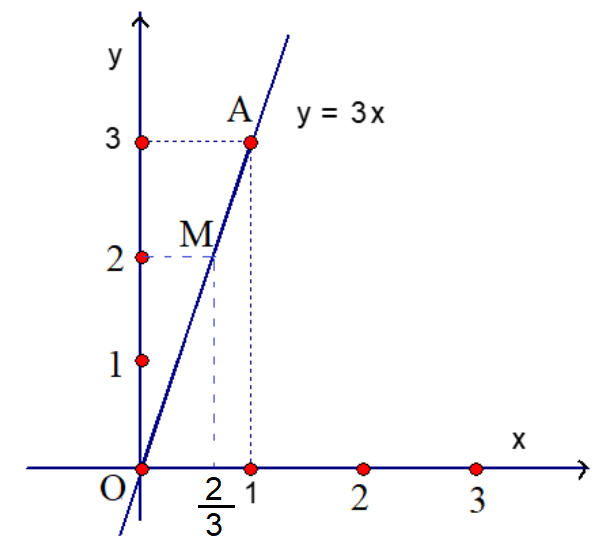
Cho đồ thị của hàm số y=(m-1/2)x (với m là hằng số, m khác 1/2 đi qua điểm A (2; 6). a) Xác định m. b) Vẽ đồ thị của hàm số đã cho với giá trị m tìm được ở câu a. Tìm trên đồ thị hàm số trên điểm có tung độ bằng 2. (ảnh 3)

Điểm có tung độ bằng 2 hay y = 2. Khi đó, $x = \frac{y}{3} = \frac{2}{3}$ .

Do đó, điểm $M (\frac{2}{3}; 2)$ thuộc đồ thị hàm số y = 3x và có tung độ bằng 2 (như hình vẽ).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

So sánh 2³⁰+ 3³⁰ + 4³⁰ và 3 . 24¹⁰.

Xem đáp án

Lời giải

Ta có: 4³⁰ = (2 . 2)³⁰ = 2³⁰. 2³⁰ = (2³)¹⁰ . (2²)¹⁵ = 8¹⁰ . 4¹⁵

Lại có: 24¹⁰ . 3 = (8 . 3)¹⁰ . 3 = 8¹⁰ . 3¹⁰. 3 = 8¹⁰ . 3¹¹

Ta thấy 4¹⁵ > 4¹¹ > 3¹¹

Suy ra 8¹⁰ . 4¹⁵ > 8¹⁰ . 3¹¹

Hay 4³⁰ > 3 . 24¹⁰

Do đó 2³⁰+ 3³⁰ + 4³⁰ > 3 . 24¹⁰.

Vậy 2³⁰ + 3³⁰ + 4³⁰ > 3 . 24¹⁰.

Câu 2

1) Cho hình vẽ sau, biết a // b và b // c. Tính số đo ${\hat{C}}_{1}$ ?

2) Cho ∆ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA.

a) Chứng minh: ∆ABD = ∆HBD.

b) Chứng minh: $D H ⊥ B C$ .

c) Giả sử $\hat{C} = 60^{o}$ . Tính số đo $\hat{A D B}$ .

Xem đáp án

Lời giải

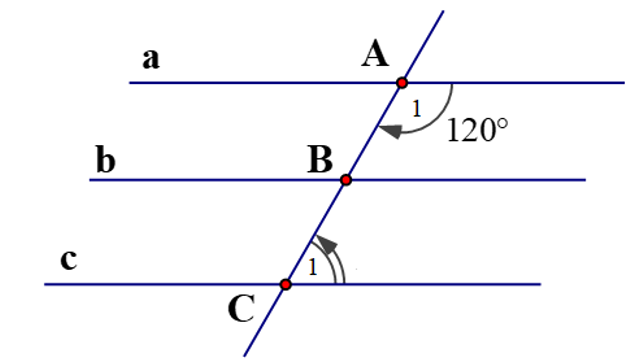
1) 1) Cho hình vẽ sau, biết a // b và b // c. Tính số đo góc C1 ? Cho ∆ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA. a) Chứng minh: ∆ABD = ∆HBD. b) Chứng minh: DH vuông góc BC. c) Giả sử góc C=60 độ . Tính số đo góc ADB (ảnh 2)

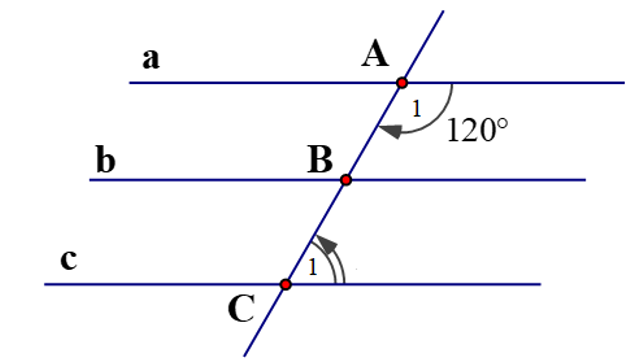
Ta có: a // b và b // c.

Suy ra: a // c (tính chất ba đường thẳng song song).

Ta lại có: ${\hat{A}}_{1}$ và ${\hat{C}}_{1}$ là hai góc trong cùng phía nên ${\hat{A}}_{1} + {\hat{C}}_{1} = 180^{o}$ .

$\Rightarrow {\hat{C}}_{1} = 180^{o} - {\hat{A}}_{1} = 180^{o} - 120^{o} = 60^{o}$ .

Vậy ${\hat{C}}_{1} = 60^{o}$ .

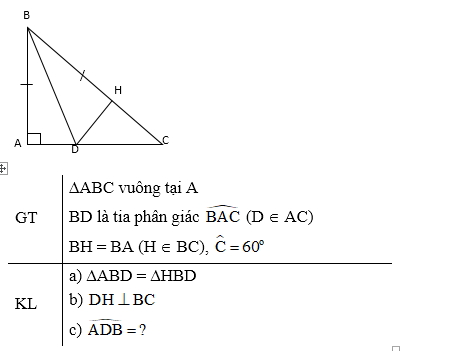
1) Cho hình vẽ sau, biết a // b và b // c. Tính số đo góc C1 ? Cho ∆ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA. a) Chứng minh: ∆ABD = ∆HBD. b) Chứng minh: DH vuông góc BC. c) Giả sử góc C=60 độ . Tính số đo góc ADB (ảnh 3)

a) Chứng minh: ∆ABD = ∆HBD.

Xét ∆ABD và ∆HBD có:

AB = BH (gt)

$\hat{A B H} = \hat{D B H}$ (vì BD là tia phân giác của $\hat{B A C}$ )

Cạnh BD chung.

Do đó ∆ABD = ∆HBD (c.g.c)

b) Chứng minh: $D H ⊥ B C$

Vì ∆ABD = ∆HBD (câu a) nên $\hat{B A D} = \hat{B H D}$ (hai góc tương ứng)

Mà $\hat{B A D} = 90^{o}$ . Do đó $\hat{B H D}$ = 90^o.

Vậy DH $⊥$ BC.

c) Tính số đo $\hat{A D B}$ .

Ta có ∆ABC vuông tại A nên $\hat{A B C} + \hat{C} = 90^{o}$ .

Mà $\hat{C} = 60^{o}$ nên $\hat{A B C} = 30^{o}$ .

Vì BD là tia phân giác của $\hat{B A C}$ .

Nên $\hat{A B D} = \hat{D B H} = \hat{A B D} : 2 = 30^{o} : 2 = 15^{o}$ .

Ta có ∆ABD vuông tại A nên $\hat{A B D} + \hat{A D B} = 90^{o}$ .

$\hat{A D B} = 90^{o} - \hat{A B D} = 90^{o} - 15^{o} = 75^{o}$

Vậy $\hat{A D B} = 75^{o}$ .

Câu 3

Ba đơn vị kinh doanh gốp vốn theo tỉ lệ 3; 5; 7. Hỏi mỗi đơn vị chia bao nhiêu lãi nếu tổng số tiền lãi là 450 triệu đồng và tiền lãi được chia tỉ lệ thuận với số vốn đã góp.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Thực hiện phép tính (Tính nhanh nếu có thể)

a) $\frac{- 2}{15} + \frac{3}{10}$

b) $9 . {(- \frac{1}{3})}^{2} + \frac{1}{6} . \sqrt{4}$

c) $15 \frac{1}{4} : \frac{5}{7} - 25 \frac{1}{4} : \frac{5}{7}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tìm x, biết:

a) $x - \frac{2}{3} = - \frac{5}{21}$

b) x² + 15 = 20

c) $\frac{2}{3} x = - \frac{5}{21}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

So sánh 2³⁰+ 3³⁰ + 4³⁰ và 3 . 24¹⁰.

Thực hiện phép tính (Tính nhanh nếu có thể)

a) $\frac{- 2}{15} + \frac{3}{10}$

b) $9 . {(- \frac{1}{3})}^{2} + \frac{1}{6} . \sqrt{4}$

c) $15 \frac{1}{4} : \frac{5}{7} - 25 \frac{1}{4} : \frac{5}{7}$

Tìm x, biết:

a) $x - \frac{2}{3} = - \frac{5}{21}$

b) x² + 15 = 20

c) $\frac{2}{3} x = - \frac{5}{21}$ .