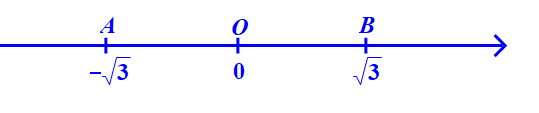Khẳng định nào dưới đây thể hiện hai đại lượng tỉ lệ thuận với nhau?
A. Chiều dài và chiều rộng của hình chữ nhật có diện tích cho trước;
B. Năng suất lao động và thời gian để làm xong một công việc;
C. Vận tốc và thời gian khi đi trên cùng một quãng đường;
D. Chu vi và bán kính của một đường tròn.
Quảng cáo
Trả lời:
Đáp án đúng là: D.
Công thức tính diện tích hình chữ nhật có chiều dài a và chiều rộng b là S = a.b. Do đó chiều dài và chiều rộng của hình chữ nhật có diện tích cho trước là hai đại lượng tỉ lệ nghịch.
Năng suất lao động và thời gian để làm xong một công việc là hai đại lượng tỉ lệ nghịch.
Công thức tính quãng đường khi di chuyển với vận tốc v và thời gian t là S = vt, do đó vận tốc và thời gian khi đi trên cùng một quãng đường là hai đại lượng tỉ lệ nghịch.
Công thức tính chu vi C của đường tròn có bán kính R là C = π.2R nên chu vi đường tròn tỉ lệ thuận với bán kính R theo hệ số tỉ lệ là π. Do đó phương án D là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Nếu \(a \in \mathbb{Q}\) thì a không thể là số vô tỉ;
B. Nếu \(a \in \mathbb{Z}\) thì a không thể là số vô tỉ;
C. Nếu \(a \in \mathbb{N}\) thì a không thể là số vô tỉ;
D. Nếu \(a \in \mathbb{R}\) thì a không thể là số vô tỉ;
Lời giải
Đáp án đúng là: D.
Tập hợp ℚ là tập hợp các số hữu tỉ nên không thể là số vô tỉ. Do đó phương án A là phát biểu đúng.
Tập hợp ℤ là tập hợp các số nguyên nên không thể là số vô tỉ. Do đó phương án B là phát biểu đúng.
Tập hợp ℕ là tập hợp các số tự nhiên nên không thể là số vô tỉ. Do đó phương án C là phát biểu đúng.
Tập hợp ℝ là tập hợp các số thực, bao gồm các số vô tỉ. Do đó phương án D là phát biểu sai.
Câu 2
A. x = 20; y = 30; z = −92;
B. x = −20; y = 30; z = 92;
C. x = 20; y = 30; z = 92;
D. x = 20; y = −30; z = 92.
Lời giải
Đáp án đúng là: C.
Từ dãy tỉ số bằng nhau \(\frac{{x + 1}}{3} = \frac{{y - 2}}{4} = \frac{{z - 1}}{{13}}\) suy ra \(\frac{{2\left( {x + 1} \right)}}{6} = \frac{{3\left( {y - 2} \right)}}{{12}} = \frac{{z - 1}}{{13}}\)
Hay \(\frac{{2x + 2}}{6} = \frac{{3y - 6}}{{12}} = \frac{{z - 1}}{{13}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{{2x + 2}}{6} = \frac{{3y - 6}}{{12}} = \frac{{z - 1}}{{13}} = \frac{{2x + 2 - \left( {3y - 6} \right) + z - 1}}{{6 - 12 + 13}} = \frac{{2x + 2 - 3y + 6 + z - 1}}{7}\)
\( = \frac{{\left( {2x - 3y + z} \right) + 7}}{7} = \frac{{42 + 7}}{7} = \frac{{49}}{7} = 7\)
Suy ra:
+) \(\frac{{2x + 2}}{6} = 7\) do đó 2x + 2 = 7.6 = 42 suy ra 2x = 42 – 2 = 40 nên x = 40 : 2 = 20;
+) \(\frac{{3y - 6}}{{12}} = 7\) do đó 3y – 6 = 7.12 = 84 suy ra 3y = 84 + 6 = 90 nên y = 90 : 3 = 30;
+) \(\frac{{z - 1}}{{13}} = 7\) do đó z – 1 = 7.13 = 91 suy ra z = 91 + 1 = 92.
Vậy x = 20; y = 30; z = 92.
Câu 3
A. 1950 kg;
B. 0,65 tấn;
C. 35 kg;
D. 6500 kg.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. x = 9; y = 18; z = 27;
B. x = −9; y = −18; z = −27;
C. x = −9; y = 18; z = 27;
D. x = −9; y = 18; z = −27.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. x = −1;
B. x = 0;
C. x = −1 hoặc x = 0;
D. x = 1;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 150 triệu đồng;
B. 300 triệu đồng;
C. 600 triệu đồng;
D. 900 triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Điểm A;
B. Điểm B;
C. Điểm O;
D. Điểm A và điểm B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.