Cho tam giác ABC cân ở A. Đường phân giác AD và trung tuyến CE cắt nhau tại H. Đường thẳng BH

P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x;    Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³.

a) P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x

P(x) = x⁴ + (3x³ - x³) + (-x - 4x) + $\frac{1}{2}$

P(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$

Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³

Q(x) = x⁴ + (-4x³ + 2x³) + (-2x - 3x) + $\frac{3}{2}$

Q(x) = x⁴ - 2x³ - 5x + $\frac{3}{2}$

b) P(x) + Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ + x⁴ - 2x³ - 5x + $\frac{3}{2}$

P(x) + Q(x) = (x⁴ + x⁴) + (2x³ - 2x³) + (-5x - 5x) + $(\frac{1}{2}-\frac{3}{2})$

P(x) + Q(x) = 2x⁴ - 10x + 1

P(x) - Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ - (x⁴ - 2x³ - 5x + $\frac{3}{2}$)

P(x) - Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ - x⁴ + 2x³ + 5x - $\frac{3}{2}$

P(x) - Q(x) = (x⁴ - x⁴) + (2x³ + 2x³) + (-5x + 5x) + $(\frac{1}{2}+\frac{3}{2})$

P(x) - Q(x) = 4x³ - 1

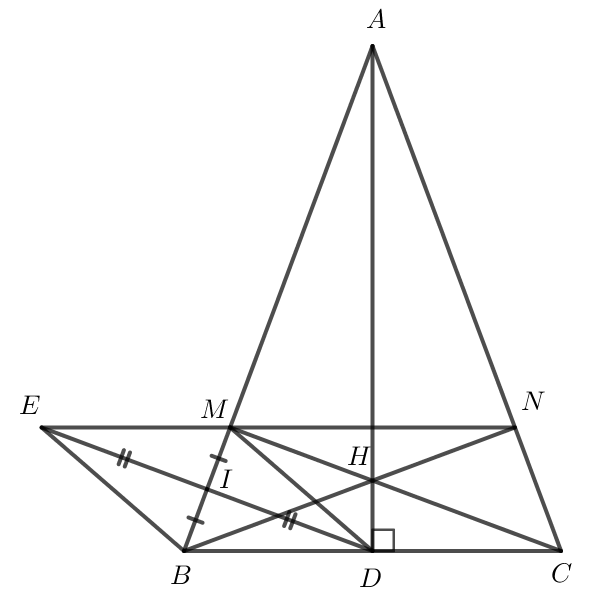
a) $\Delta ABC$ cân tại A có AD là đường cao nên AD cũng là đường trung tuyến.

Do đó D là trung điểm của BC.

Áp dụng định lý Pytago vào $\Delta AB\text{D}$ vuông tại D ta có:

AD² + BD² = AB²

$\Rightarrow$ 12² + BD² = 13²

$\Rightarrow$ BD² = 169 - 144

$\Rightarrow$ BD² = 25

$\Rightarrow$ BD = 5 cm.

Do D là trung điểm của BC nên BD = $\frac{1}{2}$BC.

Do đó BC = 10 cm.

b) Xét $\Delta DIM$ vuông tại I và $\Delta DIB$ vuông tại I có:

ID chung.

IM = IB (theo giả thiết).

$\Rightarrow \Delta DIM=\Delta DIB$ (2 cạnh góc vuông).

$\Rightarrow$ DM = DB (2 cạnh tương ứng).

Mà DB = $\frac{1}{2}$BC nên DM = $\frac{1}{2}$BC.

c) Tam giác DIM có MD = DB = DC = $\frac{1}{2}$BC nên Tam giác MBC vuông tại M

Do đó CM vuông góc với AB

Tam giác ABC  có  AD vuông góc BC, CM vuông góc AB.

Mà AD cắt CM tại H nên H là trực tâm của tam giác ABC.

Do đó: BH vuống góc AC hay BN vuông góc AC.

Do tam giác ABC cân tại A nên AB = AC và góc ABC bằng góc ACB.

Xét tam giác ANB vuông tại N và tam giác AMC vuông tại M:

Góc A chung.

AB = AC (chứng minh trên).

Tam giác ANB= tam giác AMC (cạnh huyền - góc nhọn).

Suy ra AN = AM (2 cạnh tương ứng).

tam giác AMN có AN = AM nên tam giác AMN cân tại A.

Do đó Góc AMN= góc ANM.$\widehat{AMN}+\widehat{ANM}+\widehat{MAN}=180°$

Xét Tam giác AMN có 

$\Rightarrow 2\widehat{AMN}+\widehat{MAN}=180°$

$\Rightarrow \widehat{AMN}=\frac{180°-\widehat{MAN}}{2}$ (1).

Xét tam giác ABC có $\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°$

$\Rightarrow 2\widehat{ABC}+\widehat{BAC}=180°$

$\Rightarrow \widehat{ABC}=\frac{180°-\widehat{BAC}}{2}$ (2).

Từ (1) và (2) suy ra $\widehat{AMN}=\widehat{ABC}$.

Mà hai góc này ở vị trí đồng vị nên MN // BC (3).

Xét  tam giác EIM và tam giác DIB có:

EI = DI (theo giả thiết).

Góc EIM =góc DIB (2 góc đối đỉnh).

IM = IB (theo giả thiết).

tam giác EIM= tam giác DIB (c - g - c).

$\Rightarrow \widehat{EMI}=\widehat{DBI}$ (2 góc tương ứng).

Mà hai góc này ở vị trí so le trong nên EM // BD hay EM // BC (4).

Từ (3) và (4) suy ra E, M, N thẳng hàng.

Vậy E, M, N thẳng hàng.