Câu hỏi:

19/08/2025 2,375

Cho tam giác ABC cân tại A có đường cao AD.

a) Tính BC biết AB = 13 cm và AD = 12 cm.

b) Kẻ DI vuông góc với AB tại I. Lấy điểm M trên cạnh AB sao cho I là trung điểm của đoạn thẳng BM. Chứng minh DM = $\frac{1}{2}$ BC.

c) Gọi H là giao điểm của AD và CM, N là giao điểm của BH và AC. Lấy E là điểm thuộc tia đối của tia ID sao cho ID = IE. Chứng minh 3 điểm E, M, N thẳng hàng.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra học kì 2 Toán 7 có đáp án ( Mới nhất) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

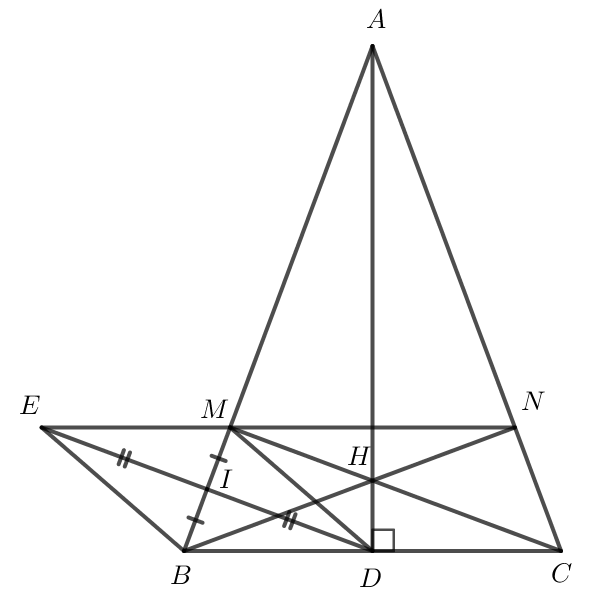
Cho tam giác ABC cân tại A có đường cao AD. a) Tính BC biết AB = 13 cm và AD = 12 cm. b) Kẻ DI vuông góc với AB tại I. Lấy điểm M trên cạnh AB sao cho I là trung điểm của đoạn thẳng BM. Chứng minh DM = BC. c) Gọi H là giao điểm của AD và CM, N là giao điểm của BH và AC. Lấy E là điểm thuộc tia đối của tia ID sao cho ID = IE. Chứng minh 3 điểm E, M, N thẳng hàng. (ảnh 1)

a) $Δ A B C$ cân tại A có AD là đường cao nên AD cũng là đường trung tuyến.

Do đó D là trung điểm của BC.

Áp dụng định lý Pytago vào $Δ A B D$ vuông tại D ta có:

AD² + BD² = AB²

$\Rightarrow$ 12² + BD² = 13²

$\Rightarrow$ BD²= 169 - 144

$\Rightarrow$ BD² = 25

$\Rightarrow$ BD = 5 cm.

Do D là trung điểm của BC nên BD = $\frac{1}{2}$ BC.

Do đó BC = 10 cm.

b) Xét $Δ D I M$ vuông tại I và $Δ D I B$ vuông tại I có:

ID chung.

IM = IB (theo giả thiết).

$\Rightarrow Δ D I M = Δ D I B$ (2 cạnh góc vuông).

$\Rightarrow$ DM = DB (2 cạnh tương ứng).

Mà DB = $\frac{1}{2}$ BC nên DM = $\frac{1}{2}$ BC.

c) Tam giác DIM có MD = DB = DC = $\frac{1}{2}$ BC nên Tam giác MBC vuông tại M

Do đó CM vuông góc với AB

Tam giác ABC có AD vuông góc BC, CM vuông góc AB.

Mà AD cắt CM tại H nên H là trực tâm của tam giác ABC.

Do đó: BH vuống góc AC hay BN vuông góc AC.

Do tam giác ABC cân tại A nên AB = AC và góc ABC bằng góc ACB.

Xét tam giác ANB vuông tại N và tam giác AMC vuông tại M:

Góc A chung.

AB = AC (chứng minh trên).

Tam giác ANB= tam giác AMC (cạnh huyền - góc nhọn).

Suy ra AN = AM (2 cạnh tương ứng).

tam giác AMN có AN = AM nên tam giác AMN cân tại A.

Do đó Góc AMN= góc ANM. $\hat{A M N} + \hat{A N M} + \hat{M A N} = 180 °$

Xét Tam giác AMN có

$\Rightarrow 2 \hat{A M N} + \hat{M A N} = 180 °$

$\Rightarrow \hat{A M N} = \frac{180 ° - \hat{M A N}}{2}$ (1).

Xét tam giác ABC có $\hat{A B C} + \hat{A C B} + \hat{B A C} = 180 °$

$\Rightarrow 2 \hat{A B C} + \hat{B A C} = 180 °$

$\Rightarrow \hat{A B C} = \frac{180 ° - \hat{B A C}}{2}$ (2).

Từ (1) và (2) suy ra $\hat{A M N} = \hat{A B C}$ .

Mà hai góc này ở vị trí đồng vị nên MN // BC (3).

Xét tam giác EIM và tam giác DIB có:

EI = DI (theo giả thiết).

Góc EIM =góc DIB (2 góc đối đỉnh).

IM = IB (theo giả thiết).

tam giác EIM= tam giác DIB (c - g - c).

$\Rightarrow \hat{E M I} = \hat{D B I}$ (2 góc tương ứng).

Mà hai góc này ở vị trí so le trong nên EM // BD hay EM // BC (4).

Từ (3) và (4) suy ra E, M, N thẳng hàng.

Vậy E, M, N thẳng hàng.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai đa thức:

P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x; Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³.

a) Thu gọn và sắp xếp các đa thức P(x), Q(x) theo lũy thừa giảm dần của biến;

b) Tính P(x) + Q(x); P(x) - Q(x).

Xem đáp án

Lời giải

P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x; Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³.

a) P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x

P(x) = x⁴ + (3x³- x³) + (-x - 4x) + $\frac{1}{2}$

P(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$

Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³

Q(x) = x⁴+ (-4x³ + 2x³) + (-2x - 3x) + $\frac{3}{2}$

Q(x) = x⁴ - 2x³ - 5x + $\frac{3}{2}$

b) P(x) + Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ + x⁴ - 2x³ - 5x + $\frac{3}{2}$

P(x) + Q(x) = (x⁴ + x⁴) + (2x³ - 2x³) + (-5x - 5x) + $(\frac{1}{2} - \frac{3}{2})$

P(x) + Q(x) = 2x⁴ - 10x + 1

P(x) - Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ - (x⁴ - 2x³ - 5x + $\frac{3}{2}$ )

P(x) - Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ - x⁴ + 2x³ + 5x - $\frac{3}{2}$

P(x) - Q(x) = (x⁴ - x⁴) + (2x³ + 2x³) + (-5x + 5x) + $(\frac{1}{2} + \frac{3}{2})$

P(x) - Q(x) = 4x³ - 1

Câu 2

Cho các đa thức

A(x) = 12x³ + 2ax + a²

B(x) = 2x² - $| 2 a + 3 |$ x + a²

Tìm a biết A(1) = B(-2).

Xem đáp án

Lời giải

A(x) = 12x³ + 2ax + a²

B(x) = 2x² - $| 2 a + 3 |$ x + a²

Với x = 1 ta có A(1) = 12.1³ + 2.a.1 + a² = 12 + 2a + a².

Với x = -2 ta có B(-2) = 2.(-2)² - $| 2 a + 3 |$ .(-2) + a² = 9 + 2 $| 2 a + 3 |$ + a².

Do A(1) = B(-2) nên 12 + 2a + a² = 9 + 2 $| 2 a + 3 |$ + a².

$\Rightarrow$ 12 + 2a + a² - 9 - a² = 2 $| 2 a + 3 |$ .

$\Rightarrow$ (12 - 9) + (a² - a²) + 2a = 2 $| 2 a + 3 |$ .

$\Rightarrow$ 3 + 2a = 2 $| 2 a + 3 |$ .

Xét 2a + 3 ≥ 0 hay a ≥ $\frac{- 3}{2}$ , khi đó $| 2 a + 3 |$ = 2a + 3.

Do đó 3 + 2a = 2(2a + 3).

$\Rightarrow$ 3 + 2a = 4a + 6

$\Rightarrow$ 2a - 4a = 6 - 3

$\Rightarrow$ -2a = 3

$\Rightarrow$ a = $\frac{- 3}{2}$ (thỏa mãn)

Xét 2a + 3 < 0 hay a < $\frac{- 3}{2}$ , khi đó $| 2 a + 3 |$ = -(2a + 3).

Do đó 3 + 2a = -2(2a + 3).

$\Rightarrow$ 3 + 2a = -4a - 6

$\Rightarrow$ 2a + 4a = -6 - 3

$\Rightarrow$ 6a = -9

$\Rightarrow$ a = $\frac{- 3}{2}$ (loại)

Vậy a= $\frac{- 3}{2}$

Câu 3

Cho tam giác ABC cân ở A. Đường phân giác AD và trung tuyến CE cắt nhau tại H. Đường thẳng BH

A. chứa phân giác trong đỉnh B.

B. chứa đường cao kẻ từ B.

C. chứa trung tuyến kẻ từ B.

D. cả ba đáp án A, B và C đều đúng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm tất cả các số nguyên dương x, y thỏa mãn:

$\frac{9}{x y} - \frac{1}{y} = 2 + \frac{3}{x}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho đa thức P(x) = x³ - 6x² + 11x - 6. Giá trị nào sau đây KHÔNG là nghiệm của P(x)?

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho đơn thức T = 3x²y³z. Đơn thức nào sau đây sau khi thu gọn đồng dạng với T.

A. x²y²zx.

B. xy²zxy.

C. x²zy²z².

D. x²yxz.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho hai đa thức:

P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x; Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³.

a) Thu gọn và sắp xếp các đa thức P(x), Q(x) theo lũy thừa giảm dần của biến;

b) Tính P(x) + Q(x); P(x) - Q(x).

Cho các đa thức

A(x) = 12x³ + 2ax + a²

B(x) = 2x² - $| 2 a + 3 |$ x + a²

Tìm a biết A(1) = B(-2).

Tìm tất cả các số nguyên dương x, y thỏa mãn:

$\frac{9}{x y} - \frac{1}{y} = 2 + \frac{3}{x}$ .

Cho đa thức P(x) = x³ - 6x² + 11x - 6. Giá trị nào sau đây KHÔNG là nghiệm của P(x)?

Cho đơn thức T = 3x²y³z. Đơn thức nào sau đây sau khi thu gọn đồng dạng với T.