Câu hỏi:
13/07/2024 4,204
a) Dựa vào đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) (H.6.2), tìm x sao cho y = 8.
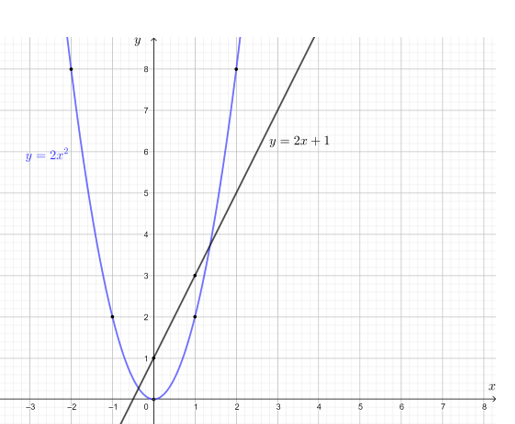
b) Vẽ đồ thị của các hàm số y = 2x + 1 và y = 2x2 trên cùng một mặt phẳng tọa độ.
a) Dựa vào đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) (H.6.2), tìm x sao cho y = 8.
b) Vẽ đồ thị của các hàm số y = 2x + 1 và y = 2x2 trên cùng một mặt phẳng tọa độ.
Câu hỏi trong đề: Bài tập Bài 15. Hàm số có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Với y = 8, từ điểm 8 trên trục Oy, ta kẻ đường thẳng song song với Ox, đường thẳng này cắt đồ thị hàm số \(y = \frac{1}{2}{x^2}\) tại hai điểm, từ hai điểm đó hạ vuông góc xuống trục Ox, ta thấy hai chân đường vuông góc trên Ox là điểm 4 và – 4.
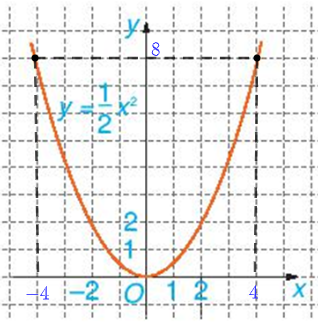
Vậy với y = 8 thì x = 4, x = – 4.
b)
+ Ta có: y = 2x + 1
Tập xác định của hàm số là \(\mathbb{R}\).
Với x = 0 thì y = 2 . 0 + 1 = 1.
Với x = 1 thì y = 2 . 1 + 1 = 3.
Do đó đồ thị hàm số y = 2x + 1 là đường thẳng đi qua 2 điểm (0; 1) và (1; 3).
+ Ta có: y = 2x2
Tập xác định của hàm số là \(\mathbb{R}\).
Bảng giá trị tương ứng của x và y
|
x |
0 |
1 |
– 1 |
2 |
– 2 |
|
y = 2x2 |
0 |
2 |
2 |
8 |
8 |
Trên mặt phẳng tọa độ, vẽ đường cong đi qua các điểm (0; 0), (1; 2), (– 1; 2), (2; 8), (– 2; 8), đường cong này chính là đồ thị của hàm số y = 2x2.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Biểu thức 2x3 + 3x + 1 có nghĩa với mọi \(x \in \mathbb{R}\).
Vậy tập xác định của hàm số là D = \(\mathbb{R}\).
b) Biểu thức \(\frac{{x - 1}}{{{x^2} - 3x + 2}}\)có nghĩa khi x2 – 3x + 2 ≠ 0 (1).
Ta có: x2 – 3x + 2 = x2 – x – 2x + 2 = x(x – 1) – 2(x – 1) = (x – 1)(x – 2).
Khi đó: (1) ⇔ (x – 1)(x – 2) ≠ 0 ⇔ x – 1 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ 1 và x ≠ 2.
Vậy tập xác định của hàm số là D = \(\mathbb{R}\backslash \left\{ {1;\,\,2} \right\}\).
c) Biểu thức \(\sqrt {x + 1} + \sqrt {1 - x} \) có nghĩa khi \(\left\{ \begin{array}{l}x + 1 \ge 0\\1 - x \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\x \le 1\end{array} \right. \Leftrightarrow - 1 \le x \le 1\)
Vậy tập xác định của hàm số là D = [– 1; 1].
Lời giải
Hướng dẫn giải
a) Ta có: x + y = 1 ⇒ y = – x + 1.
Với mỗi giá trị thực của x, ta đều xác định được một và chỉ một giá trị thực của y.
Vậy trong trường hợp này y là hàm số của x.
b) y = x2
Với mỗi giá trị thực của x, ta đều xác định được một và chỉ một giá trị thực của y.
Vậy trong trường hợp này y là hàm số của x.
c) y2 = x
Ta có: với x = 1 thì y2 = 1, suy ra y = 1 hoặc y = – 1, do đó với một giá trị của x, ta xác định được 2 giá trị của y, vậy trong trường hợp này y không phải là hàm số của x.
d) x2 – y2 = 0
Suy ra: y2 = x2.
Với x = 1 ⇒ x2 = 12 = 1, suy ra y2 = 1, khi đó y = 1 hoặc y = – 1, do đó với một giá trị của x, ta xác định được 2 giá trị của y, vậy trong trường hợp này y không phải là hàm số của x.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)