Câu hỏi:

27/06/2022 245

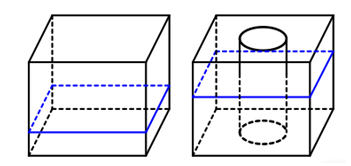
Một hình hộp chữ nhật có chiều cao là 90 cm, đáy hộp là hình chữ nhật có chiều rộng là 50 cm và chiều dài là 80 cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là 40 cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính đáy là 20 cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu?

A. 68,32 cm.

B. 78,32 cm.

C. 58,32 cm.

D. 48,32 cm.

Xem lời giải

Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án C

Trước khi đặt vào khối hộp một khối trụ thì thể tích lượng nước có trong khối hộp là:

\[{V_n} = 40.80.50 = 160000\left( {c{m^3}} \right)\].

Gọi \[h\left( {cm} \right)\] là chiều cao của mực nước so với đáy.

Sau khi đặt vào khối hộp một khối trụ thì thể tích lượng nước là: \[{V_n} = h.\left( {4000 - 400\pi } \right)\left( {c{m^3}} \right)\]

Do lượng nước không đổi nên ta có: \[\begin{array}{l}h.\left( {4000 - 400\pi } \right) = 160000\\ \Leftrightarrow h = \frac{{160000}}{{4000 - 400\pi }} \approx 58,32\;\left( {cm} \right).\end{array}\]

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz, có tất cả bao nhiêu giá trị nguyên của m để \[{x^2} + {y^2} + {z^2} + 2\left( {m + 2} \right)x - 2\left( {m - 1} \right)z + 3{m^2} - 5 = 0\] là phương trình của một mặt cầu?

A. 4.

B. 6.

C. 5.

D. 7.

Lời giải

Đáp án D

Phương trình đã cho là phương trình của một mặt cầu

\[ \Leftrightarrow {\left( {m + 2} \right)^2} + {\left( {m + 1} \right)^2} - 3{m^2} + 5 > 0 \Leftrightarrow {m^2} - 2m - 10 < 0 \Leftrightarrow 1 - \sqrt {11} < m < 1 + \sqrt {11} \].

Do \[m \in \mathbb{Z}\] nên \[m \in \left\{ { - 2; - 1;0;1;2;3;4} \right\}\]. Vậy có 7 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Câu 2

Phương trình \[{7^{2{x^2} + 5x + 4}} = 49\] có tổng tất cả các nghiệm bằng:

A. 1.

B. \[\frac{5}{2}.\]

C. \[ - 1.\]

D. \[ - \frac{5}{2}.\]

Lời giải

Đáp án D

Phương pháp:

Đưa về cùng cơ số: \[{a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow f\left( x \right) = g\left( x \right)\;\left( {0 < a \ne 1} \right)\].

Cách giải:

Ta có \[{7^{2{x^2} + 5x + 4}} = 49 = {7^2} \Leftrightarrow 2{x^2} + 5x + 4 = 2 \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = - 2\end{array} \right..\]

Vậy tổng các nghiệm của phương trình là \[ - \frac{1}{2} - 2 = - \frac{5}{2}.\]

Câu 3

Trong không gian với hệ tọa độ Oxyz, viết phương trình tham số của đường thẳng đi qua điểm \[M\left( {1;2;3} \right)\] và song song với giao tuyến của hai mặt phẳng \[\left( P \right):3x + y - 3 = 0,\left( Q \right):2x + y + z = 0\].

A. \[\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 3t\\z = 3 + t\end{array} \right..\]

B. \[\left\{ \begin{array}{l}x = 1 + t\\y = 2 - 3t\\z = 3 - t\end{array} \right..\]

C. \[\left\{ \begin{array}{l}x = 1 - t\\y = 2 - 3t\\z = 3 + t\end{array} \right..\]

D. \[\left\{ \begin{array}{l}x = 1 + t\\y = 2 - 3t\\z = 3 + t\end{array} \right..\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian với hệ tọa độ Oxyz, cho điểm \[A\left( {0;1;0} \right)\] và mặt phẳng \[\left( Q \right):x + y - 4z - 6 = 0\] và đường thẳng \[d:\left\{ \begin{array}{l}x = 3\\y = 3 + t\\z = 5 - t\end{array} \right.\]. Phương trình mặt phẳng qua A song song với d và vuông góc với mặt phẳng \[\left( Q \right)\] là:

A. \[x - 2y + z + 2 = 0.\]

B. \[3x - y - z + 1 = 0.\]

C. \[x + y + z - 1 = 0.\]

D. \[3x + y + z - 1 = 0.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số \[f\left( x \right)\] có \[f\left( 1 \right) = 1\] và \[f'\left( x \right) = - \frac{{\ln x}}{{{x^2}}},\forall x > 0\]. Khi đó \[\int\limits_1^e {f\left( x \right)dx} \] bằng:

A. \[\frac{3}{2}.\]

B. \[\frac{2}{e} - 1.\]

C. \[ - \frac{3}{2}.\]

D. \[1 - \frac{2}{e}.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian tọa độ Oxyz, cho mặt cầu \[\left( S \right):{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 16\]. Mặt phẳng \[\left( P \right)\] thay đổi luôn đi qua điểm \[A\left( {2;1;9} \right)\] và tiếp xúc với mặt cầu \[\left( S \right)\]. Đặt M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm O đến \[\left( P \right)\]. Giá trị M + m bằng:

A. 8.

B. \[8\sqrt 3 .\]

C. 9.

D. \[\sqrt {15} .\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian Oxyz, cho \[\overrightarrow {OA} = \overrightarrow i - 2\overrightarrow j + 3\overrightarrow k \], điểm \[B\left( {3; - 4;1} \right)\] và điểm \[C\left( {2;0; - 1} \right)\]. Tọa độ trọng tâm của tam giác ABC là:

A. \[\left( {1; - 2;3} \right).\]

B. \[\left( { - 2;2;1} \right).\]

C. \[\left( {2; - 2;1} \right).\]

D. \[\left( { - 1;2; - 3} \right).\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Trong không gian Oxyz, có tất cả bao nhiêu giá trị nguyên của m để \[{x^2} + {y^2} + {z^2} + 2\left( {m + 2} \right)x - 2\left( {m - 1} \right)z + 3{m^2} - 5 = 0\] là phương trình của một mặt cầu?

Phương trình \[{7^{2{x^2} + 5x + 4}} = 49\] có tổng tất cả các nghiệm bằng:

Trong không gian với hệ tọa độ Oxyz, viết phương trình tham số của đường thẳng đi qua điểm \[M\left( {1;2;3} \right)\] và song song với giao tuyến của hai mặt phẳng \[\left( P \right):3x + y - 3 = 0,\left( Q \right):2x + y + z = 0\].

Cho hàm số \[f\left( x \right)\] có \[f\left( 1 \right) = 1\] và \[f'\left( x \right) = - \frac{{\ln x}}{{{x^2}}},\forall x > 0\]. Khi đó \[\int\limits_1^e {f\left( x \right)dx} \] bằng:

Trong không gian Oxyz, cho \[\overrightarrow {OA} = \overrightarrow i - 2\overrightarrow j + 3\overrightarrow k \], điểm \[B\left( {3; - 4;1} \right)\] và điểm \[C\left( {2;0; - 1} \right)\]. Tọa độ trọng tâm của tam giác ABC là:

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu