Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
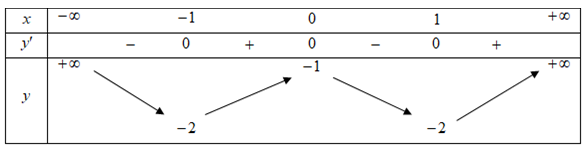
Số điểm cực tiểu của hàm số \[g\left( x \right) = 2{f^3}\left( x \right) + 4{f^2}\left( x \right) + 1\] là:
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Đáp án C
Ta có: \[g'\left( x \right) = 6{f^2}\left( x \right).f'\left( x \right) + 8f\left( x \right).f'\left( x \right) \Leftrightarrow g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\f\left( x \right) = 0\\f\left( x \right) = - \frac{4}{3}\end{array} \right..\]
Với \[f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 1\end{array} \right.;\;f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1} < 1\\x = {x_2} > 1\end{array} \right.;\;f\left( x \right) = - \frac{4}{3} \Leftrightarrow \left[ \begin{array}{l}x = {x_3},{x_3} > {x_1}\\x = {x_4} \in \left( { - 1;0} \right)\\x = {x_5} \in \left( {0;1} \right)\\x = {x_6} > 1,{x_6} < {x_2}\end{array} \right..\]
Vì \[\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \] nên ta có bảng biến thiên cho \[g\left( x \right)\] như sau:
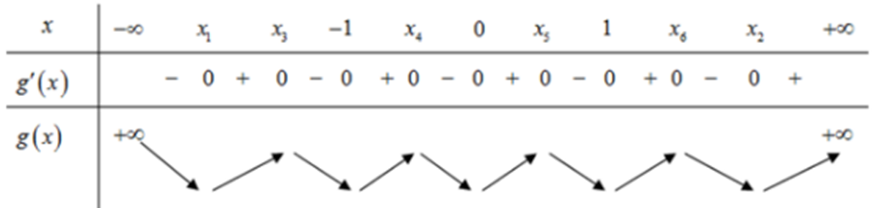
Từ đây ta suy ra số điểm cực tiểu của hàm số \[g\left( x \right)\] là 5.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D
Phương trình đã cho là phương trình của một mặt cầu
\[ \Leftrightarrow {\left( {m + 2} \right)^2} + {\left( {m + 1} \right)^2} - 3{m^2} + 5 > 0 \Leftrightarrow {m^2} - 2m - 10 < 0 \Leftrightarrow 1 - \sqrt {11} < m < 1 + \sqrt {11} \].
Do \[m \in \mathbb{Z}\] nên \[m \in \left\{ { - 2; - 1;0;1;2;3;4} \right\}\]. Vậy có 7 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 2
Lời giải
Đáp án D
Phương pháp:
Đưa về cùng cơ số: \[{a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow f\left( x \right) = g\left( x \right)\;\left( {0 < a \ne 1} \right)\].
Cách giải:
Ta có \[{7^{2{x^2} + 5x + 4}} = 49 = {7^2} \Leftrightarrow 2{x^2} + 5x + 4 = 2 \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = - 2\end{array} \right..\]
Vậy tổng các nghiệm của phương trình là \[ - \frac{1}{2} - 2 = - \frac{5}{2}.\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.