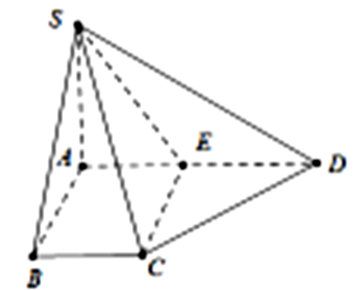
Cho hình chóp S.ABCD có SA vuông góc với đáy, \[SA = a\sqrt 6 .\] Đáy ABCD là hình thang vuông tại A và \[B,{\mkern 1mu} {\mkern 1mu} AB = BC = \frac{1}{2}AD = a.\] Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp \[S.ECD\].
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Đáp án B
Ta có: \({\rm{CE // AB}} \Rightarrow {\rm{CE}} \bot A{\rm{D}}\)
Mặt khác \(CE \bot {\rm{S}}A \Rightarrow CE \bot \left( {SE{\rm{D}}} \right)\)
\( \Rightarrow {R_{C.SE{\rm{D}}}} = \sqrt {\frac{{C{E^2}}}{4} + {{\left( {{R_{S{\rm{D}}E}}} \right)}^2}} \)
Lại có \(CE = AB = a,{\rm{ }}\sin \widehat {SE{\rm{A}}} = \sin \widehat {SE{\rm{D}}}\)
\[ = \frac{{SA}}{{SE}} = \frac{{a\sqrt 6 }}{{\sqrt {{a^2} + 6{{\rm{a}}^2}} }} = \frac{{a\sqrt 6 }}{{\sqrt 7 }}\]
\( \Rightarrow {R_{SE{\rm{D}}}} = \frac{{S{\rm{D}}}}{{2\sin \widehat {SE{\rm{D}}}}} = \frac{{a\sqrt {10} }}{{2.\frac{{a\sqrt 6 }}{{\sqrt 7 }}}} = \frac{{a\sqrt {105} }}{6}\)
Vậy \({R_{S.C{\rm{D}}E}} = a\sqrt {\frac{{19}}{6}} \).
Cách 2: Do \(\left( {SE{\rm{D}}} \right) \bot \left( {CE{\rm{D}}} \right) \Rightarrow R = \sqrt {R_1^2 + R_2^2 - \frac{{G{T^2}}}{4}} \) trong đó \({R_1} = {R_{SE{\rm{D}}}} = \frac{{a\sqrt {105} }}{6}\),
\({R_2} = {R_{CE{\rm{D}}}} = \frac{{C{\rm{D}}}}{2} = \frac{{a\sqrt 2 }}{2}\) và \(GT = E{\rm{D}} = a \Rightarrow R = a\sqrt {\frac{{19}}{6}} \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án D
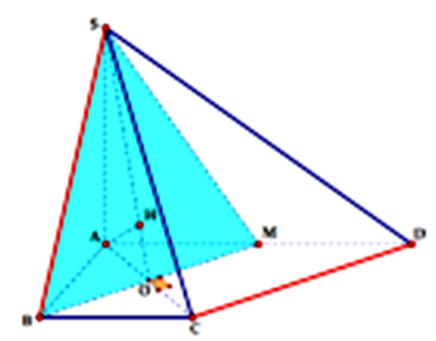
Gọi M là trung điểm \(A{\rm{D}} \Rightarrow M{\rm{D}} = BC = \frac{{A{\rm{D}}}}{2}\) và \(M{\rm{D // BC }} \Rightarrow {\rm{MD}}CB\) là hình bình hành.
\( \Rightarrow d\left( {C{\rm{D}};SB} \right) = d\left( {D;(SBM)} \right) = d\left( {A;(SBM)} \right)\)
Gọi \(O = BM \cap AC\). Dễ dàng chứng minh AMCB là hình vuông \( \Rightarrow AC \bot BM\)
tại theo giao tuyến SO.
Trong \(\left( {SAO} \right)\), kẻ \(AH \bot {\rm{S}}O \Rightarrow AH \bot \left( {SBM} \right) \Rightarrow AH = d\left( {A;(SBM)} \right)\)
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{O^2}}} = \frac{1}{{A{C^2}}} + \frac{1}{{\frac{{A{C^2}}}{4}}} = \frac{5}{{A{C^2}}} = \frac{5}{{2{a^2}}} \Rightarrow AH = \frac{{a\sqrt {10} }}{5}\).
Câu 2
Lời giải
Đáp án B
Chọn ra 2 học sinh nam có \(C_{10}^2\) cách, chọn ra 3 học sinh nữ có \(C_{15}^3\) cách.
Theo quy tắc nhân có \(C_{10}^2.C_{15}^3\) cách để chọn ra 2học sinh nam và 3 học sinh nữ để lập thành một đội 5 bạn đi biểu diễn văn nghệ.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.