Cho hình lăng trụ \[ABC.A'B'C'\] có thể tích làV, gọi M, N lần lượt là trung điểm của \[A'C'\] và \[B'C'\], G là trọng tâm tam giác \[ABC,\] mặt phẳng \[\left( {MNG} \right)\] chia khối lăng trụ đã cho thành hai phần, thể tích khối đa diện chứa đỉnh C′ là
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Đáp án D
Do \(MN{\rm{ /
![Cho hình lăng trụ \[ABC.A'B'C'\] có thể tích làV, gọi M, N lần lượt là trung điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/06/blobid16-1656396757.png)
/ A'B' // AB}}\) nên mặt phẳng \(\left( {MNG} \right)\) cắt AC và BC tại Q, P thì \(PQ{\rm{ // MN // AB}}\).
Gọi \(S = {S_{ABC}}\); h là chiều cao khối lăng trụ.
Ta thấy \(MNC'.QPC\) là khối chóp cụt.
\({S_1} = {S_{C'NM}} = \frac{S}{4};{\rm{ }}{{\rm{S}}_2} = {S_{CPQ}} = \frac{2}{3}.\frac{2}{3}S = \frac{4}{9}S\)
Do đó \({V_{MNC'.QPC}} = \frac{h}{3}\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right) = \frac{{37}}{{108}}S.h = \frac{{37}}{{108}}V\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án D
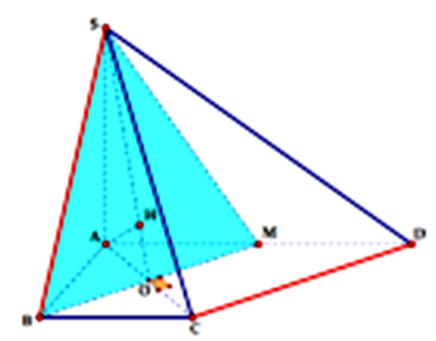
Gọi M là trung điểm \(A{\rm{D}} \Rightarrow M{\rm{D}} = BC = \frac{{A{\rm{D}}}}{2}\) và \(M{\rm{D // BC }} \Rightarrow {\rm{MD}}CB\) là hình bình hành.
\( \Rightarrow d\left( {C{\rm{D}};SB} \right) = d\left( {D;(SBM)} \right) = d\left( {A;(SBM)} \right)\)
Gọi \(O = BM \cap AC\). Dễ dàng chứng minh AMCB là hình vuông \( \Rightarrow AC \bot BM\)
tại theo giao tuyến SO.
Trong \(\left( {SAO} \right)\), kẻ \(AH \bot {\rm{S}}O \Rightarrow AH \bot \left( {SBM} \right) \Rightarrow AH = d\left( {A;(SBM)} \right)\)
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{O^2}}} = \frac{1}{{A{C^2}}} + \frac{1}{{\frac{{A{C^2}}}{4}}} = \frac{5}{{A{C^2}}} = \frac{5}{{2{a^2}}} \Rightarrow AH = \frac{{a\sqrt {10} }}{5}\).
Câu 2
Lời giải
Đáp án B
Chọn ra 2 học sinh nam có \(C_{10}^2\) cách, chọn ra 3 học sinh nữ có \(C_{15}^3\) cách.
Theo quy tắc nhân có \(C_{10}^2.C_{15}^3\) cách để chọn ra 2học sinh nam và 3 học sinh nữ để lập thành một đội 5 bạn đi biểu diễn văn nghệ.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.