Câu hỏi:
12/07/2024 649
Cho tam giác ABC như trong Hình 8a.
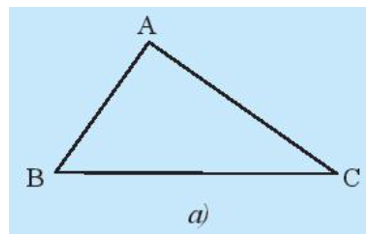
Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’ có , B’A’ = BA, B’C’ = BC theo các bước:
- Vẽ .
- Trên tia B’x lấy đoạn B’A’ = BA.
- Trên tia B’y lấy đoạn B’C’ = BC.
Vẽ đoạn A’C’, ta được tam giác A’B’C’ (Hình 8b).
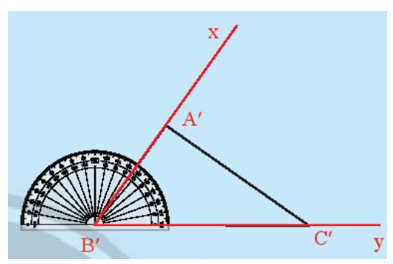
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Cho tam giác ABC như trong Hình 8a.
Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’ có , B’A’ = BA, B’C’ = BC theo các bước:
- Vẽ .
- Trên tia B’x lấy đoạn B’A’ = BA.
- Trên tia B’y lấy đoạn B’C’ = BC.
Vẽ đoạn A’C’, ta được tam giác A’B’C’ (Hình 8b).
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Câu hỏi trong đề:
Bài tập Bài 2. Tam giác bằng nhau có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thực hiện theo các bước sau:
Bước 1: Vẽ tia B’y.
Bước 2: Vẽ tia B’x sao cho .
Bước 3: Trên tia B’x lấy đoạn B’A’ = BA; trên tia B’y lấy đoạn B’C’ = BC.
Bước 4: Vẽ đoạn A’C’ ta được tam giác A’B’C’.
Cắt rời tam giác A’B’C’ ra khỏi tờ giấy, ta thấy tam giác A’B’C’ chồng khít tam giác ABC.
Trong trường hợp này, hai tam giác A’B’C’ và ABC bằng nhau.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC.
b) DEAB = DECD.
c) OE là tia phân giác của góc xOy.
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC.
b) DEAB = DECD.
c) OE là tia phân giác của góc xOy.
Xem đáp án »
12/07/2024
21,168
Câu 2:
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm của CD.
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm của CD.
Xem đáp án »
12/07/2024
8,813
Câu 3:
Cho biết DMNP = DDEF và MN = 4 cm, MP = 5 cm, EF = 6 cm. Tìm chu vi tam giác MNP.
Cho biết DMNP = DDEF và MN = 4 cm, MP = 5 cm, EF = 6 cm. Tìm chu vi tam giác MNP.
Xem đáp án »
12/07/2024
4,309
Câu 4:
Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó , . Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại.
Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó , . Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại.
Xem đáp án »
12/07/2024
3,363
Câu 5:
Cho DDEF = DHIK và = 73o, DE = 5 cm, IK = 7 cm. Tính số đo và độ dài HI, EF.
Cho DDEF = DHIK và = 73o, DE = 5 cm, IK = 7 cm. Tính số đo và độ dài HI, EF.
Xem đáp án »
12/07/2024
2,826
Câu 6:
Cho . Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong
. Nối O với P (Hình 16). Hãy chứng minh rằng DOMP = DONP, từ đó suy ra OP là tia phân giác của .
Cho . Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong
. Nối O với P (Hình 16). Hãy chứng minh rằng DOMP = DONP, từ đó suy ra OP là tia phân giác của .
Xem đáp án »
12/07/2024
2,570
Câu 7:
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) DEFH = DHGE.
b) EF // HG.
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) DEFH = DHGE.
b) EF // HG.
Xem đáp án »
12/07/2024
2,010
về câu hỏi!