Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và có bảng biến thiên như sau

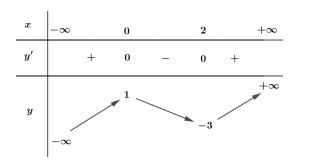
Hàm số \[y = f\left( {{x^2} - 2x} \right)\] nghịch biến trên khoảng nào dưới đây?

Đáp án B

Khi bắt đầu tiếp đất vật chuyển động được quảng đường là \(s = 162m\).

Ta có: \(s = \int\limits_0^t {\left( {10t - {t^2}} \right)dt} = \left. {\left( {5{t^2} - \frac{{{t^3}}}{3}} \right)} \right|_0^t = 5{t^2} - \frac{{{t^3}}}{3}\) (trong đó t là thời điểm vật tiếp đất).

Cho \(5{t^2} - \frac{{{t^3}}}{3} = 162 \Rightarrow t = 9\) (Do \(v\left( t \right) = 10t - {t^2} \Rightarrow 0 \le t \le 10\)).

Khi đó vận tốc của vật là: \(v\left( 9 \right) = 10.9 - {9^2} = 9{\rm{ }}\left( {{\rm{m/p}}} \right)\).

Đáp án C

+ Chia cả 2 vế của bất phương trình cho \({2^x} > 0\).

+ Đặt \(t = {\left( {3 + \sqrt 7 } \right)^x}{\rm{ }}\left( {t > 0} \right)\).

+ Đưa bất phương trình về dạng \(m \le f\left( t \right),{\rm{ }}\forall t > 0 \Leftrightarrow m \le \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( t \right)\).

+ Lập BBT hàm số \(y = f\left( t \right)\) và kết luận.

Chia cả 2 vế của bất phương trình cho \({2^x} > 0\) ta được: \({\left( {3 + \sqrt 7 } \right)^x} + \left( {2 - m} \right){\left( {\frac{{3 - \sqrt 7 }}{2}} \right)^x} - \left( {m + 1} \right) \ge 0\)

Nhận xét: \({\left( {3 + \sqrt 7 } \right)^x}{\left( {\frac{{3 - \sqrt 7 }}{2}} \right)^x} = 1\), do đó khi ta đặt \(t = {\left( {3 + \sqrt 7 } \right)^x}{\rm{ }}\left( {t > 0} \right) \Rightarrow {\left( {\frac{{3 - \sqrt 7 }}{2}} \right)^x} = \frac{1}{t}\).

Phương trình trở thành: \(t + \left( {2 - m} \right)\frac{1}{t} - \left( {m + 1} \right) \ge 0 \Leftrightarrow {t^2} - \left( {m + 1} \right)t + 2 - m \ge 0\)

\( \Leftrightarrow {t^2} - t + 2 \ge m\left( {t + 1} \right) \Leftrightarrow m \le \frac{{{t^2} - t + 2}}{{t + 1}} = f\left( t \right){\rm{ }}\forall t > 0 \Leftrightarrow m \le \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( t \right)\).

Xét hàm số \(f\left( t \right) = \frac{{{t^2} - t + 2}}{{t + 1}}\left( {t > 0} \right)\), ta có: \(f'\left( t \right) = \frac{{\left( {2t - 1} \right)\left( {t + 1} \right) - {t^2} + t - 2}}{{{{\left( {t + 1} \right)}^2}}} = \frac{{{t^2} + 2t - 3}}{{{{\left( {t + 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = - 3\end{array} \right.\).

BBT:

Từ BBT \( \Rightarrow m \le 1\).

Kết hợp điều kiện đề bài \( \Rightarrow \left\{ \begin{array}{l}m \in \mathbb{R}\\m \in \left[ { - 10;1} \right]\end{array} \right. \Rightarrow \) có 12 giá trị của m thỏa mãn yêu cầu bài toán.