a) Cho đơn thức A = −3xy2−23x2y2 Thu gọn rồi tính giá trị của A tại x = –1; y = 12 b) Tìm đa thức Q biết: (2x2 – y2 + 34xy) + Q = x2 – 2y2 + 34xy.

a) Ta có: A= −3xy2−23x2y2=−3xy249x4y2=−3.49.x.x4.y2.y2=−43x5y4 Thay x = –1 , y = đơn thức A =−43x5y4 ta được: A=−43.−15.124=112 Vậy A=112 tại x=−1 và y=12 b) Ta có: (2x2 – y2 + xy) + Q = x2 – 2y2 + xy ⇒Q=x2−2x2+−2y2+y2+34xy−34xy ⇒Q=−x2−y2

Câu hỏi:

19/08/2025 552

a) Cho đơn thức A = $(- 3 x y^{2}) {(- \frac{2}{3} x^{2} y)}^{2}$ Thu gọn rồi tính giá trị của A tại x = –1; y = $\frac{1}{2}$

b) Tìm đa thức Q biết:
(2x² – y² + $\frac{3}{4}$ xy) + Q = x² – 2y² + $\frac{3}{4}$ xy.

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Ta có: A= $(- 3 x y^{2}) {(- \frac{2}{3} x^{2} y)}^{2}$ $= - 3 x y^{2} (\frac{4}{9} x^{4} y^{2}) = (- 3. \frac{4}{9}) . (x . x^{4}) . (y^{2} . y^{2}) = - \frac{4}{3} x^{5} y^{4}$

Thay x = –1 , y = đơn thức A = $- \frac{4}{3} x^{5} y^{4}$ ta được: $A = - \frac{4}{3} . {(- 1)}^{5} . {(\frac{1}{2})}^{4} = \frac{1}{12}$

Vậy $A = \frac{1}{12}$ tại $x = - 1$ và $y = \frac{1}{2}$

b) Ta có: $(2 x 2 - y 2 + x y) + Q = x 2 - 2 y 2 + x y$

$\Rightarrow Q = (x^{2} - 2 x^{2}) + (- 2 y^{2} + y^{2}) + (\frac{3}{4} x y - \frac{3}{4} x y)$

$\Rightarrow Q = - x^{2} - y^{2}$

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai đa thức P(x) = 2x³ – 2x + x² + 3x + 2.

Q(x) = 4x³ – 3x² – 3x + 4x – 3x³ + 4x² + 1.

a) Thu gọn P(x), Q(x);

b) Chứng tỏ x = –1 là nghiệm của P(x), Q(x);

c) Tính R(x) sao cho Q(x) + R(x) = P(x).

Xem đáp án

Lời giải

a) P(x) = 2x³ – 2x + x² + 3x + 2

= 2x³ + x² + (–2x + 3x) + 2

= 2x³ + x² + x + 2 (0,25 điểm)

Q(x) = 4x³ – 3x²– 3x + 4x – 3x³ + 4x² + 1

= (4x³ – 3x³) + (–3x² + 4x²) + (–3x + 4x) + 1

= x³ + x²+ x + 1 (0,25 điểm)

b) +) x = –1 là nghiệm của P(x) vì:

P(–1) = 2(–1)³ +(–1)² +(–1) + 2 = –2 + 1 – 1 + 2 = 0. (0,25 điểm)

+) x = –1 là nghiệm của Q(x) vì:

Q(–1) = (–1)³ +(–1)² +(–1) + 1 = –1 + 1 – 1 + 1 = 0. (0,25 điểm)

c) Ta có: Q(x) + R(x) = P(x)

R(x) = P(x) – Q(x)

= (2x³ + x² + x + 2) – (x³ + x²+ x + 1)

= 2x³ + x² + x + 2 – x³ – x²– x – 1

= (2x³ – x³) + (x² – x²) + (x – x) + (2 – 1)

= x³ + 1

Vậy R(x) = x³ + 1.

Câu 2

Cho $Δ A B C$ cân tại A ( $\hat{A} < 90^{0}$ ).

Kẻ BD $⊥$ AC (D $⊥$ AC), CE $⊥$ AB (E $\in$ AB), BD và CE cắt nhau tại H.

a) Chứng minh: BD = CE;

b) Chứng minh: $Δ B H C$ cân;

c) Chứng minh: AH là đường trung trực của BC;

d) Trên tia BD lấy điểm K sao cho D là trung điểm của BK. So sánh: $\hat{E C B}$ và

$\hat{D K C}$

.

Xem đáp án

Lời giải

Vẽ hình đúng

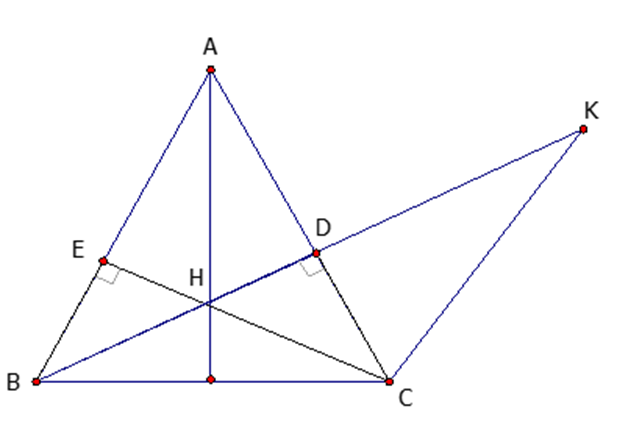
Cho cân tại A (). Kẻ BDAC (DAC), CE AB (E AB), BD và CE cắt nhau tại H. a) Chứng minh: BD = CE; b) Chứng minh: cân; c) Chứng minh: AH là đường trung trực của BC; d) Trên tia BD lấy điểm K sao cho D là trung điểm của BK. So sánh: và . (ảnh 1)

a) Xét tam giác BDC vuông tại D và tam giác CEB vuông tại E có:

BC cạnh chung

$\hat{A B C} = \hat{A C B}$ (tam giác ABC cân tại A)

Do đó: $Δ B D C = Δ C E B (c . h - g . n)$

Suy ra: BD = CE (hai cạnh tương ứng) (1 điểm)

b) $Δ H B C$ có $\hat{D B C} = \hat{E C B}$ $Δ B D C = Δ C E B$

Nên tam giác HBC cân ở H. (1 điểm)

c) Vì H là giao hai đường cao BD và CE trong tam giác ABC

Nên AH là đường cao thứ ba của tam giác ABC

Mà tam giác ABC cân tại A

Do đó AH là đường trung trực của BC.

d) Tam giác CBK có CD vừa là đường trung tuyến (D là trung điểm của BK) vừa là đường cao nên tam giác CBK cân ở C

Suy ra: $\hat{C B H} = \hat{D K C}$ (góc ở đáy)

Mà: $\hat{C B H} = \hat{E C B}$ $Δ B D C = Δ C E B$

Do đó:

\hat{E C B} = \hat{D K C}

Câu 3

Cho đa thức: f(x) = x³ + ax² + bx – 2 Xác định a, b biết đa thức có 2 nghiệm là x₁ = –1 và x₂ = 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

1. Tìm x biết:

a) (x – 8)(x³ + 8) = 0;

b) (4x – 3) – (x + 5) = 3(10 – x).

2. Cho hai đa thức sau: f(x) = (x – 1)(x + 2) và g(x) = x³ + ax² + bx + 2.

Xác định a và b biết nghiệm của đa thức f(x) cũng là nghiệm của đa thức g(x).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một giáo viên theo dõi thời gian giải bài toán (tính theo phút) của một lớp học và ghi lại:

10

5

4

7

7

7

4

7

9

10

6

8

6

10

8

9

6

8

7

7

9

7

8

8

6

8

6

6

8

7

a) Dấu hiệu cần tìm hiểu ở đây là gì?

b) Lập bảng tần số và tìm Mốt của dấu hiệu;

c) Tính thời gian trung bình của lớp.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

a) Cho đơn thức A = $(- 3 x y^{2}) {(- \frac{2}{3} x^{2} y)}^{2}$ Thu gọn rồi tính giá trị của A tại x = –1; y = $\frac{1}{2}$

b) Tìm đa thức Q biết:
(2x² – y² + $\frac{3}{4}$ xy) + Q = x² – 2y² + $\frac{3}{4}$ xy.

Cho hai đa thức P(x) = 2x³ – 2x + x² + 3x + 2.

Q(x) = 4x³ – 3x² – 3x + 4x – 3x³ + 4x² + 1.

a) Thu gọn P(x), Q(x);

b) Chứng tỏ x = –1 là nghiệm của P(x), Q(x);

c) Tính R(x) sao cho Q(x) + R(x) = P(x).

Cho đa thức: f(x) = x³ + ax² + bx – 2 Xác định a, b biết đa thức có 2 nghiệm là x₁ = –1 và x₂ = 1.

1. Tìm x biết:

a) (x – 8)(x³ + 8) = 0;

b) (4x – 3) – (x + 5) = 3(10 – x).

2. Cho hai đa thức sau: f(x) = (x – 1)(x + 2) và g(x) = x³ + ax² + bx + 2.

Xác định a và b biết nghiệm của đa thức f(x) cũng là nghiệm của đa thức g(x).