Câu hỏi:

19/08/2025 9,833

Cho hai biểu thức $A = \frac{x + x^{2}}{2 - x}$ và $B = \frac{2 x}{x + 1} + \frac{3}{x - 2} - \frac{2 x^{2} + 1}{x^{2} - x - 2}$

a) Tính giá trị của A khi |2x – 3| = 1.

b) Tìm điều kiện xác định và rút gọn biểu thức B.
c) Tìm số nguyên x để P = A.B đạt giá trị lớn nhất.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra giữa kì 2 Toán 8 có đáp án ( Mới nhất) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) $A = \frac{x + x^{2}}{2 - x}$

Điều kiện xác định của biểu thức A là: 2 – x ≠ 0 Û x ≠ 2.

Ta có |2x – 3| = 1

Trường hợp 1: 2x – 3 ≥ 0 thì 2x – 3 = 1

Với 2x – 3 ≥ 0 Û 2x ≥ 3 Û x ≥ $\frac{3}{2}$ thì |2x – 3| = 2x – 3. Khi đó:

2x – 3 = 1 Û 2x = 4 Û x = 2 (không thõa mãn)

Trường hợp 2: 2x – 3 ≤ 0 Û 2x ≤ 3 Û x ≤ $\frac{3}{2}$ thì |2x – 3| = – 2x + 3. Khi đó:

– 2x + 3 = 1 Û 2x = 2 Û x = 1 (thõa mãn)

Thay x = 1 (TMĐK) vào $A = \frac{x + x^{2}}{2 - x}$ ta được:

$A = \frac{1 + 1^{2}}{2 - 1} = \frac{1 + 1}{1} = 2$ .

Vậy khi |2x – 3| = 1 thì A = 2.

b) Điều kiện xác định của biểu thức B:

$\{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \\ x^{2} - x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \\ x^{2} + x - 2 x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \\ (x + 1) (x - 2) \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq - 1 \\ x \neq 2 \end{matrix}$

Khi đó, ta có:

$B = \frac{2 x}{x + 1} + \frac{3}{x - 2} - \frac{2 x^{2} + 1}{x^{2} - x - 2} = \frac{2 x (x - 2)}{(x + 1) (x - 2)} + \frac{3 (x + 1)}{(x - 2) (x + 1)} - \frac{2 x^{2} + 1}{(x - 2) (x + 1)} = \frac{2 x^{2} - 4 x}{(x + 1) (x - 2)} + \frac{3 x + 3}{(x - 2) (x + 1)} - \frac{2 x^{2} + 1}{(x - 2) (x + 1)} = \frac{2 x^{2} - 4 x + 3 x + 3 - (2 x^{2} + 1)}{(x + 1) (x - 2)} = \frac{2 x^{2} - 4 x + 3 x + 3 - 2 x^{2} - 1}{(x + 1) (x - 2)} = \frac{2 x^{2} - 2 x^{2} - 4 x + 3 x + 3 - 1}{(x + 1) (x - 2)} = \frac{- x + 2}{(x + 1) (x - 2)} = \frac{- (x - 2)}{(x + 1) (x - 2)} = \frac{- 1}{x + 1}$

Vậy

B = \frac{- 1}{x + 1}

c) Ta có P = A.B nên:

$P = \frac{x + x^{2}}{2 - x} . \frac{- 1}{x + 1} = \frac{x (x + 1)}{2 - x} . \frac{- 1}{x + 1} = \frac{- x}{2 - x} = \frac{x}{x - 2} = 1 + \frac{2}{x - 2}$

Để biểu thức $P = 1 + \frac{2}{x - 2}$ đạt giá trị lớn nhất thì $\frac{2}{x - 2}$ đạt giá trị lớn nhất.

Suy ra (x – 2) đạt giá trị nhỏ nhất.

∙ Xét x – 2 < 0 hay x < 2 thì $\frac{2}{x - 2}$ < 0.

Do đó không xác định được giá trị nhỏ nhất trong trường hợp này.

∙ Xét x – 2 > 0 hay x > 2 thì $\frac{2}{x - 2}$ > 0.

Ta thấy: x là số nguyên lớn hơn 2 mà (x – 2) đạt giá trị nhỏ nhất nên x = 3.

Vậy để P = A . B đạt giá trị lớn nhất thì x = 3.

Đang tải chế độ Học...

Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC có AB = 5 cm; BC = 8 cm. Trên cạnh AB lấy điểm D sao cho AD = 2 cm. Qua D kẻ đường thẳng song song với BC cắt AC ở E và cắt đường thẳng qua C song song với AB ở F.

a) Tính DE.

b) BF cắt AC ở I. Tính $\frac{I F}{I B}$ .

c) Chứng minh rằng IC² = IE.IA.
d) BE cắt AF ở H. Tính $\frac{H A}{H F}$ .

Xem đáp án

Lời giải

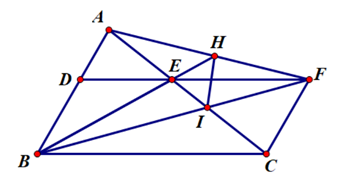
Cho tam giác ABC có AB = 5 cm; BC = 8 cm. Trên cạnh AB lấy điểm D sao cho AD = 2 cm. (ảnh 1)

a)Áp dụng định lý Ta-let trong ∆ABC có DE // BC, ta có:

$\frac{A D}{A B} = \frac{D E}{B C}$

$\Leftrightarrow D E = \frac{A D . B C}{A B} = \frac{2.8}{5} = 3, 2$ (cm).

b) Theo đề ta có DE // BC hay DF // BC và BD // CF.

Suy ra tứ giác BDFC là hình bình hành nên ta có FC = BD.

Mà BD = AB – AD = 5 – 2 = 3 (cm).

Suy ra FC = 3 cm.

Ta có CF // AD (gt), áp dụng hệ quả của định lý Ta-let, ta có:

$\frac{I F}{I B} = \frac{F C}{A D} = \frac{3}{5}$

c) Áp dụng hệ quả của định lý Ta – let với CF // AD, ta có:

$\frac{I F}{I B} = \frac{I C}{I A}$ (1)

Áp dụng hệ quả định lý Ta – let với EF // BC, ta có:

$\frac{I F}{I B} = \frac{I E}{I C}$ (2)

Từ (1) và (2) suy ra $\frac{I C}{I A} = \frac{I E}{I C} = \frac{I F}{I B}$ nên IC² = IE.IA.

Câu 2

Giải bài toán bằng cách lập phương trình

Một người đi xe máy từ A đến B với vận tốc 30 km/h. Khi đến B người đó nghỉ 30 phút rồi quay trở về A với vận tốc 40 km/h. Tính quãng đường AB biết thời gian cả đi, về và nghỉ là 5 giờ 10 phút ?

Xem đáp án

Lời giải

Gọi x (km) là độ dài quãng đường AB (x > 0).

Một người đi xe máy từ A đến B với vận tốc 30 km/h nên thời gian người đó từ A đến B là $\frac{x}{30}$ (h).

Người đó đi B về A với vận tốc 40 km/h nên thời gian để đi từ B về A là $\frac{x}{40}$ (h).

Thời gian người đó nghỉ là: 30 phút = $\frac{1}{2}$ h.

Đổi 5 giờ 10 phút = $\frac{31}{6}$ giờ.

Theo đề bài, tổng thời gian người đó đi, quay về và nghỉ là 5 giờ 10 phút nên ta có phương trình:

$\frac{x}{30} + \frac{x}{40} + \frac{1}{2} = \frac{31}{6} \Leftrightarrow \frac{x .4}{30.4} + \frac{x .3}{40.3} + \frac{1.60}{2.60} = \frac{31.20}{6.20} \Leftrightarrow \frac{4 x}{120} + \frac{3 x}{120} + \frac{60}{120} = \frac{620}{120}$

Û 4x + 3x + 60 = 620

Û 7x = 620 – 60

Û 7x = 560

Û x = 560 : 7

Û x = 80 (thỏa mãn điều kiện)

Vậy độ dài quãng đường AB là 80 km.

Câu 3

a) Tìm giá trị nhỏ nhất của $Q = \frac{x^{2} - 4 x + 1}{x^{2}}$ .
b) Tìm $a, b, c \in ℕ $ : $(a - \frac{1}{b}) (b - \frac{1}{c}) (c - \frac{1}{a}) \in ℕ $ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải phương trình

a) $\frac{x + 1}{3} + \frac{1}{2} = \frac{x - 1}{6} - 1$ ;

b) 4x² – 1 – x(2x – 1) = 0;

c) $\frac{x + 3}{x - 3} + \frac{x - 3}{x + 3} = \frac{x^{2} + 2 x}{x^{2} - 9} + 1$ ;
d) (x² + x – 1)(x² + x + 3) = 5.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

a) Tìm giá trị nhỏ nhất của $Q = \frac{x^{2} - 4 x + 1}{x^{2}}$ .
b) Tìm $a, b, c \in ℕ $ : $(a - \frac{1}{b}) (b - \frac{1}{c}) (c - \frac{1}{a}) \in ℕ $ .

Giải phương trình

a) $\frac{x + 1}{3} + \frac{1}{2} = \frac{x - 1}{6} - 1$ ;

b) 4x² – 1 – x(2x – 1) = 0;

c) $\frac{x + 3}{x - 3} + \frac{x - 3}{x + 3} = \frac{x^{2} + 2 x}{x^{2} - 9} + 1$ ;
d) (x² + x – 1)(x² + x + 3) = 5.