Câu hỏi:

19/08/2025 3,148

Cho tam giác ABC cân tại A có đường cao AH (H thuộc BC). Gọi M là trung điểm của đoạn thẳng AB. Gọi E là điểm đối xứng với H qua M.

Trên tia đối của tia HA lấy điểm F. Kẻ $H K ⊥ F C$ (K thuộc FC). Gọi I, Q lần lượt là trung điểm của HK, KC. Chứng minh rằng: $B K ⊥ F I$ .

Xem lời giải

Câu hỏi trong đề: Bộ 14 đề thi Học kì 1 Toán 8 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp:

Sử dụng tính chất đường trung bình của tam giác và quan hệ từ vuông góc đến song song.

Cách giải:

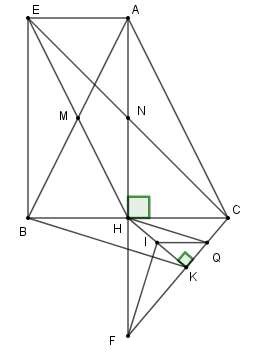
Xét tam giác HKC có I, Q lần lượt là trung điểm cạnh HK, CQ nên IQ là đường trung bình $△ H K C$

$\Rightarrow I Q // H C$ (tính chất)

Mà $H C ⊥ H F \Rightarrow I Q ⊥ H F$

Xét tam giác HFO có $I Q ⊥ H F (c m t), H K ⊥ F Q (g t)$ mà $I \in H K \Rightarrow$ I là trực tâm của $△ H F Q$

$\Rightarrow F I ⊥ H Q$

Xét tam giác BCK có H, Q lần lượt là trung điểm cạnh BC, CQ nên HQ là đường trung bình $△ B C K$

$\Rightarrow H Q // B K$ mà $F I ⊥ H Q (c m t)$

$\Rightarrow B K ⊥ F I$ (đpcm)

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm x biết: ${(x + 3)}^{2} - x^{2} = 45$

Xem đáp án

Lời giải

Phương pháp:

Sử dụng hằng đẳng thức sau đó rút gọn vế trái đưa về dạng tìm x thường gặp.

Cách giải:

${(x + 3)}^{2} - x^{2} = 45$

$\begin{array}{l} \Leftrightarrow x^{2} + 6 x + 9 - x^{2} = 45 \\ \Leftrightarrow 6 x = 36 \\ \Leftrightarrow x = 6 \end{array}$

Vậy $x = 6$ .

Câu 2

Phân tích đa thức thành nhân tử: $x^{3} - 7 x^{2} + 10 x$

Xem đáp án

Lời giải

Phương pháp:

Đặt nhân tử chung rồi tách hạng tử để nhóm các hạng tử thích hợp.

Cách giải:

$x^{3} - 7 x^{2} + 10 x$

$\begin{array}{l} = x (x^{2} - 7 x + 10) \\ = x (x^{2} - 2 x - 5 x + 10) \\ = x [x (x - 2) - 5 (x - 2)] \\ = x (x - 5) (x - 2) \end{array}$

Câu 3

Cho $a + b + c = 0 (a \neq 0; b \neq 0; c \neq 0)$ . Tính giá trị của biểu thức $A = \frac{a^{2}}{a^{2} - b^{2} - c^{2}} + \frac{b^{2}}{b^{2} - c^{2} - a^{2}} + \frac{c^{2}}{c^{2} - a^{2} - b^{2}}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC cân tại A có đường cao AH (H thuộc BC). Gọi M là trung điểm của đoạn thẳng AB. Gọi E là điểm đối xứng với H qua M

Chứng minh tứ giác AHBE là hình chữ nhật.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hai biểu thức: $A = \frac{x^{2} - 9}{3 (x + 5)}$ và $B = \frac{x}{x + 3} + \frac{2 x}{x - 3} - \frac{3 x^{2} + 9}{x^{2} - 9}$ với $x \neq - 5; x \neq \pm 3.$

Cho P= A.B. Tìm giá trị nguyên của x để P có giá trị nguyên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Rút gọn biểu thức: $x (1 - x) + (x + 1) (x - 2)$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Tìm x biết: ${(x + 3)}^{2} - x^{2} = 45$

Phân tích đa thức thành nhân tử: $x^{3} - 7 x^{2} + 10 x$

Cho $a + b + c = 0 (a \neq 0; b \neq 0; c \neq 0)$ . Tính giá trị của biểu thức $A = \frac{a^{2}}{a^{2} - b^{2} - c^{2}} + \frac{b^{2}}{b^{2} - c^{2} - a^{2}} + \frac{c^{2}}{c^{2} - a^{2} - b^{2}}$

Cho tam giác ABC cân tại A có đường cao AH (H thuộc BC). Gọi M là trung điểm của đoạn thẳng AB. Gọi E là điểm đối xứng với H qua M

Chứng minh tứ giác AHBE là hình chữ nhật.

Cho hai biểu thức: $A = \frac{x^{2} - 9}{3 (x + 5)}$ và $B = \frac{x}{x + 3} + \frac{2 x}{x - 3} - \frac{3 x^{2} + 9}{x^{2} - 9}$ với $x \neq - 5; x \neq \pm 3.$

Cho P= A.B. Tìm giá trị nguyên của x để P có giá trị nguyên.

Rút gọn biểu thức: $x (1 - x) + (x + 1) (x - 2)$