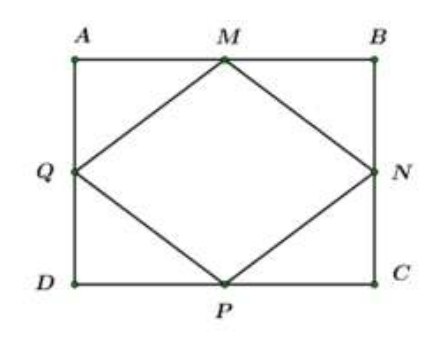
Một nền nhà hình chữ nhật ABCD có chiều dài 6,4 mét và chiều rộng 4,8 mét, người ta dự định trải lên nền nhà này một tấm thảm hình thoi có 4 đỉnh lần lượt là trung điểm M, N, P, Q của các cạnh hình chữ nhật ABCD. Tính cạnh của tấm thảm hình thoi đó.

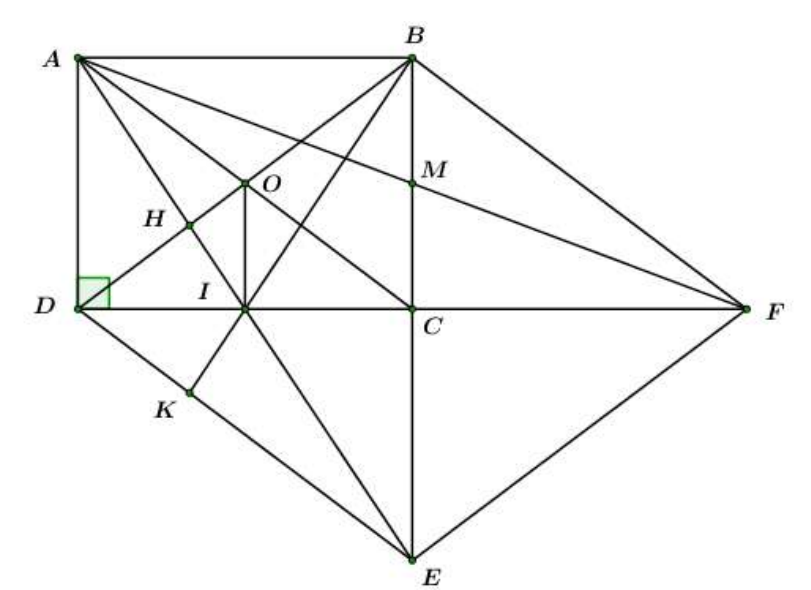
Gọi I là giao điểm của AE và DC. Tia BI cắt DE tại K. Chứng minh $KI=\frac{1}{6}AE$ .

Gọi $AC\cap BD=\left\{H\right\};AI\cap BD=O.$

Ta có: ACED là hình bình hành (cmt).

Mà $AE\cap CD=\left\{I\right\}\Rightarrow$ I là trung điểm của CD.

Lại có: O là trung điểm của AC

 $\Rightarrow$H là trực tâm của

$\Rightarrow \frac{IH}{AI}=\frac{1}{3}.$

Mà I là trung điểm của AE $\Rightarrow AI=\frac{1}{2}AE\Rightarrow IH=\frac{1}{6}AE.$

Ta có: BDEF là hình thoi (cmt)

$\Rightarrow$ DF là tia phân giác của  (tính chất hình thoi).

$\Rightarrow \angle BDC=\angle CDE.$

Ta có: BDEF là hình thoi (cmt) $\Rightarrow BD=DE$ (hai cạnh bên).

Xét $\Delta BDI$ và $\Delta EDI$ ta có:

DI chung

 $\angle IDB=\angle IDE\left(cmt\right)$

$BD=DE\left(cmt\right)$

$\Rightarrow \Delta BDI=\Delta EDI$ (c – g – c).

 $\Rightarrow \angle DBI=\angle DEI$ (hai góc tương ứng).

Và $IE=IB$ (hai cạnh tương ứng).

Xét $\Delta HBI$ và $\Delta KEI$ ta có:

$\angle HBI=\angle KEI\left(cmt\right)$

$IE=IB\left(cmt\right)$

$\angle HIB=\angle KIE$ (hai góc đối đỉnh)

$\Rightarrow \Delta HBI=\Delta KEI$ (g – c – g).

$\Rightarrow HI=IK.$

$\Rightarrow IK=\frac{1}{6}AE\left(dpcm\right).$