Siêu phẩm 30 đề thi thử THPT quốc gia 2024 do thầy cô VietJack biên soạn, chỉ từ 100k trên Shopee Mall.
Quảng cáo
Trả lời:
Phương pháp:
Dựa vào quy tắc nhân đa thức với đa thức và công thức:
Cách giải:
Ta có:
Vậy với mọi
Quảng cáo
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một nền nhà hình chữ nhật ABCD có chiều dài 6,4 mét và chiều rộng 4,8 mét, người ta dự định trải lên nền nhà này một tấm thảm hình thoi có 4 đỉnh lần lượt là trung điểm M, N, P, Q của các cạnh hình chữ nhật ABCD. Tính cạnh của tấm thảm hình thoi đó.
Câu 3:
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B qua C.
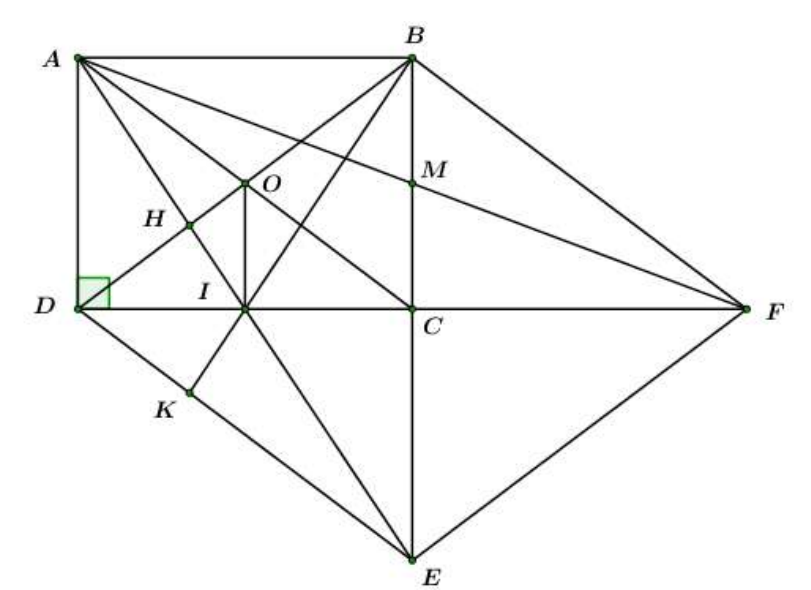
Gọi I là giao điểm của AE và DC. Tia BI cắt DE tại K. Chứng minh
Câu 4:
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B qua C.
Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác BDEF là hình thoi.
Câu 6:
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B qua C.
Chứng minh tứ giác ACED là hình bình hành.
Câu 7:
Chỉ số khối cơ thể - thường được biết đến với chữ viết tắt BMI theo tên tiếng Anh Body Mass Index - được dùng để đánh giá mức độ gầy hay béo của một người. Chỉ số này do nhà bác học người Bỉ Adolphe Quetelet đưa ra năm 1832.
Gọi W là khối lượng của một người (tính bằng kg) và H là chiều cao của người đó (tính bằng mét), chỉ số khối cơ thể BMI được tính theo công thức:
Anh Nam cao 170 cm và cân nặng là 85kg. Dựa vào thông tin trên và bảng phân loại bên, em hãy tính chỉ số BMI của anh Nam và cho biết phân loại tình trạng dinh dưỡng ở mức nào?
|
về câu hỏi!