Cho ∆ABC cân tại A, M là trung điểm BC. Gọi D, E lần lượt là hình chiếu của M trên AB và AC. Kết luận nào sau đây đúng?
Cho ∆ABC cân tại A, M là trung điểm BC. Gọi D, E lần lượt là hình chiếu của M trên AB và AC. Kết luận nào sau đây đúng?
A. \[\widehat {BMD} = \widehat {CME}\];
B. AD = AE;
C. BD = CE;
D. Cả A, B, C đều đúng.
Quảng cáo
Trả lời:
Đáp án đúng là: D
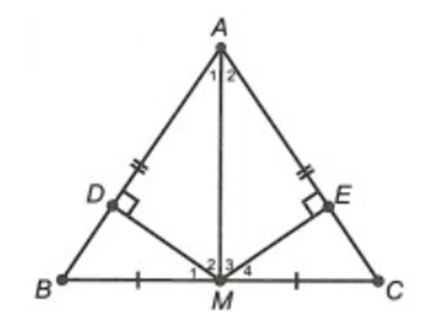
Xét ∆BDM và ∆CEM, có:
\[\widehat {BDM} = \widehat {CEM} = 90^\circ \].
\[\widehat {DBM} = \widehat {ECM}\] (∆ABC cân tại A).
MB = MC (M là trung điểm BC).
Do đó ∆BDM = ∆CEM (cạnh huyền – góc nhọn).
Suy ra BD = CE và \[\widehat {BMD} = \widehat {CME}\] (cặp cạnh và cặp góc tương ứng).
Do đó đáp án A, C đúng.
Xét ∆ADM và ∆AEM, có:
\[\widehat {ADM} = \widehat {AEM} = 90^\circ \].
AM là cạnh chung.
DM = EM (∆BDM = ∆CEM).
Do đó ∆ADM = ∆AEM (cạnh huyền – cạnh góc vuông).
Suy ra AD = AE (cặp cạnh tương ứng).
Do đó đáp án B đúng.
Vậy ta chọn đáp án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. DA = DB;
B. DA = BC;
C. DA = DB = BC;
D. DB > BC.
Lời giải
Đáp án đúng là: D
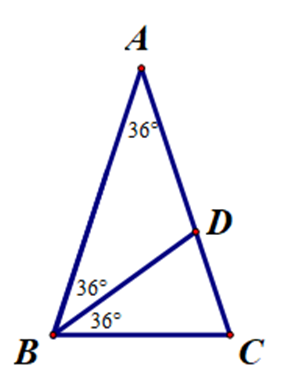
Vì ∆ABC cân tại A nên \[\widehat {ABC} = \widehat {ACB}\].
∆ABC có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \].
Suy ra \[2\widehat {ABC} = 180^\circ - \widehat {BAC} = 180^\circ - 36^\circ = 144^\circ \].
Do đó \[\widehat {BCA} = \widehat {ABC} = 72^\circ \].
Vì BD là phân giác của \[\widehat {ABC}\].
Nên \[\widehat {ABD} = \widehat {DBC} = \frac{{72^\circ }}{2} = 36^\circ \].
Ta có \[\widehat {ABD} = \widehat {BAD} = 36^\circ \].
Nên ∆ABD cân tại D.
Suy ra DA = DB (1).
Do đó đáp án A đúng.
∆ABD cân tại D: \[\widehat {ADB} = 180^\circ - \widehat {ABD} - \widehat {BAD} = 180^\circ - 36^\circ - 36^\circ = 108^\circ \].
Ta có \[\widehat {ADB} + \widehat {BDC} = 180^\circ \] (hai góc kề bù).
Suy ra \[\widehat {BDC} = 180^\circ - \widehat {ADB} = 180^\circ - 108^\circ = 72^\circ \].
Ta có \[\widehat {BDC} = \widehat {BCD} = 72^\circ \].
Suy ra ∆BCD cân tại B.
Do đó BD = BC (2).
Do đó đáp án D sai.
Từ (1), (2), ta suy ra DA = DB = BC.
Do đó đáp án B, C đúng.
Vậy ta chọn đáp án D.
Câu 2
A. DE ⊥ BC;
B. CE ⊥ BC;
C. CE ⊥ AB;
D. CE ⊥ AC.
Lời giải
Đáp án đúng là: C
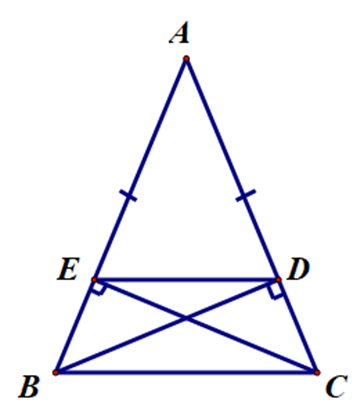
Vì ∆ABC cân tại A nên AB = AC.
Mà AE = AD (giả thiết).
Do đó AB – AE = AC – AD.
Suy ra EB = DC.
Xét ∆CBE và ∆BCD, có:
BC là cạnh chung.
EB = DC (chứng minh trên).
\[\widehat {EBC} = \widehat {DCB}\] (∆ABC cân tại A).
Do đó ∆CBE = ∆BCD (cạnh – góc – cạnh).
Suy ra \[\widehat {CEB} = \widehat {BDC} = 90^\circ \] (cặp góc tương ứng).
Khi đó ta có CE ⊥ BE hay CE ⊥ AB.
Do đó đáp án C đúng.
Vì A, B, C tạo thành một tam giác và CE ⊥ AB.
Nên CE không vuông góc với BC và CE không vuông góc với AC.
Do đó đáp án B, D sai.
∆ADE có AE = AD.
Suy ra ∆ADE cân tại A.
Do đó \[\widehat {AED} = \widehat {ADE}\].
∆ADE có: \[\widehat {BAC} + \widehat {AED} + \widehat {ADE} = 180^\circ \].
Suy ra \[2\widehat {AED} = 180^\circ - \widehat {BAC}\] (1).
∆ABC có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \].
Suy ra \[2\widehat {ABC} = 180^\circ - \widehat {BAC}\] (2).
Từ (1), (2), ta suy ra \[\widehat {AED} = \widehat {ABC}\].
Mà hai góc này ở vị trí đồng vị.
Do đó DE // BC.
Suy ra đáp án A sai.
Vậy ta chọn đáp án C.
Câu 3
A. AD > AE;
B. AD = AE;
C. AD < AE;
D. DK > KE.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Chỉ (I) đúng;
B. Chỉ (II) đúng;
C. Cả (I), (II) đều sai;
D. Cả (I), (II) đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. BD = CE;
B. CB là tia phân giác \[\widehat {ACE}\];
C. BD > CE;
D. Cả hai đáp án A, B đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\widehat {BDC} < \widehat {BEC}\];
B. BE = CD;
C. BD > EC;
D. \[\widehat {ABE} \ne \widehat {ACD}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.