Chọn phát biểu sai trong các phát biểu sau.
Chọn phát biểu sai trong các phát biểu sau.
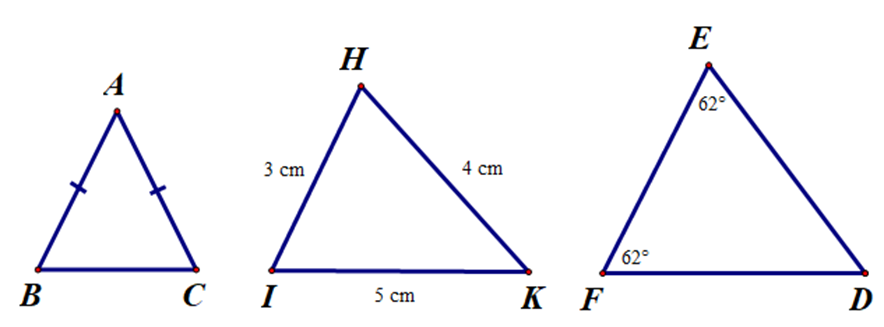
A. Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có ba cạnh bằng nhau;
B. Để nhận biết và chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó hai góc bằng nhau;
C. Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có một góc bằng 60°;
D. Để nhận biết và chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó có hai góc bằng nhau.
Quảng cáo
Trả lời:
Đáp án đúng là: C
Đáp án A, B, D đúng.
Đáp án C sai. Sửa lại:
Cách sửa 1: Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có hai góc bằng 60°;
Cách sửa 2: Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó là một tam giác cân và có một góc bằng 60°.
Vậy ta chọn đáp án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. ∆DBF cân tại B;
B. ∆DBF cân tại F;
C. ∆DBF cân tại D;
D. ∆DBF đều.
Lời giải
Đáp án đúng là: C
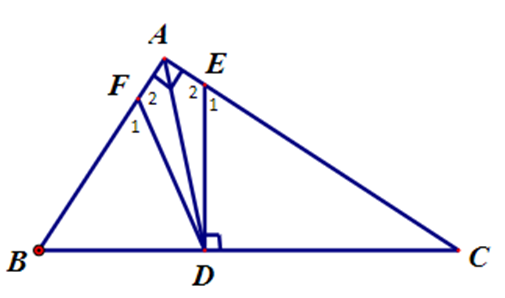
Xét ∆EAD và ∆FAD, có:
AF = AE (giả thiết).
\[\widehat {FAD} = \widehat {DAE}\] (AD là phân giác \[\widehat {BAC}\]).
AD là cạnh chung.
Do đó ∆EAD = ∆FAD (cạnh – góc – cạnh).
Suy ra \[\widehat {{E_2}} = \widehat {{F_2}}\].
Ta có \[\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ \] (hai góc kề bù).
Lại có \[\widehat {{F_1}} + \widehat {{F_2}} = 180^\circ \] (hai góc kề bù).
Do đó ta có \[\widehat {{E_1}} = \widehat {{F_1}}\] (1).
∆ABC vuông tại A: \[\widehat {ABC} + \widehat {ACB} = 90^\circ \].
∆CDE vuông tại D: \[\widehat {DEC} + \widehat {ACB} = 90^\circ \].
Do đó \[\widehat {ABC} = \widehat {DEC}\] hay \[\widehat {FBD} = \widehat {{E_1}}\] (2).
Từ (1), (2), ta suy ra \[\widehat {FBD} = \widehat {{F_1}}\].
Do đó ∆FBD cân tại D.
Vậy ta chọn đáp án C.
Câu 2
A. ∆DEF đều;
B. ∆DEF là tam giác vuông tại D;
C. ∆DEF là tam giác vuông cân tại F;
D. ∆DEF là tam giác vuông tại E.
Lời giải
Đáp án đúng là: A
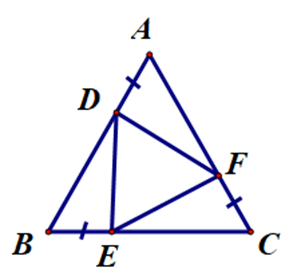
Vì ba điểm A, D, B thẳng hàng nên BD = AB – AD.
Vì ba điểm A, F, C thẳng hàng nên AF = AC – CF.
Ta có AB = AC (∆ABC đều) và AD = CF (giả thiết).
Do đó AB – AD = AC – CF.
Suy ra BD = AF.
Xét ∆ADF và ∆BED, có:
AD = BE (giả thiết).
BD = AF (chứng minh trên).
Do đó ∆ADF = ∆BED (cạnh – góc – cạnh).
Suy ra \[\widehat {FDA} = \widehat {DEB}\] (cặp góc tương ứng).
Xét ∆BDE, có: \[\widehat {BDE} + \widehat {EBD} + \widehat {DEB} = 180^\circ \].
Suy ra \[\widehat {BDE} + 60^\circ + \widehat {FDA} = 180^\circ \] (∆ABC đều).
Mà \[\widehat {BDE} + \widehat {EDF} + \widehat {FDA} = 180^\circ \] (kề bù).
Do đó \[\widehat {EDF} = 60^\circ \].
Chứng minh tương tự, ta được \[\widehat {DEF} = 60^\circ \].
Ta suy ra ∆DEF đều.
Do đó đáp án A đúng.
∆DEF là tam giác đều nên ∆DEF không thể là tam giác vuông (vì tam giác đều có các góc bằng nhau và cùng bằng 60°).
Do đó ta loại đáp án B, C, D.
Vậy ta chọn đáp án A.
Câu 3
A. ∆IBC là tam giác cân tại I;
B. ∆IBC là tam giác cân tại B;
C. ∆IBC là tam giác cân tại C;
D. ∆IBC là tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. ∆AMN cân tại A;
B. ∆AMN cân tại M;
C. ∆AMN cân tại N;
D. ∆AMN cân tại B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
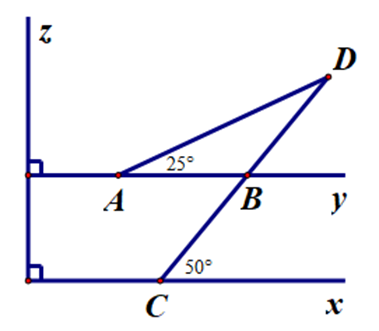
A. ∆ACD;
B. ∆ABD;
C. ∆BCD;
D. Hình vẽ bên không có tam giác nào cân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. ∆ABC là tam giác cân tại A;
B. ∆ABC là tam giác cân tại B;
C. ∆ABC là tam giác là cân tại C;
D. ∆ABC là tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.