Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
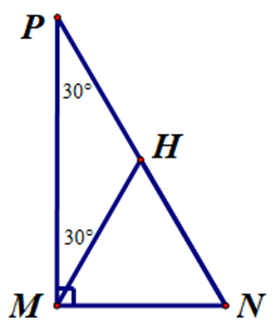
Ta có \[\widehat {PMN} = 90^\circ \] (∆MNP vuông tại M).
Suy ra \[\widehat {PMH} + \widehat {HMN} = 90^\circ \].
Do đó \[\widehat {HMN} = 90^\circ - \widehat {PMH} = 90^\circ - 30^\circ = 60^\circ \] (1).
∆MNP vuông tại M: \[\widehat {MNH} + \widehat {MPH} = 90^\circ \].
Suy ra \[\widehat {MNH} = 90^\circ - \widehat {MPH} = 90^\circ - 30^\circ = 60^\circ \] (2).
Từ (1), (2), ta suy ra ∆MNH là tam giác đều.
Do đó đáp án D đúng.
Đáp án A sai vì ∆MNP là tam giác vuông tại M.
Đáp án B sai vì ba điểm P, N, H là ba điểm thẳng hàng nên không thể tạo thành một tam giác.
Đáp án C sai vì \[\widehat {MPH} = \widehat {PMH} = 30^\circ \] nên ∆MPH cân tại H.
Vậy ta chọn đáp án D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. ∆DBF cân tại B;
B. ∆DBF cân tại F;
C. ∆DBF cân tại D;
D. ∆DBF đều.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
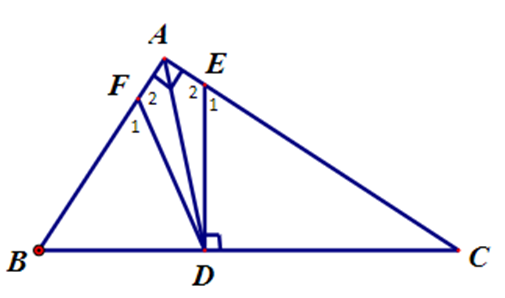
Xét ∆EAD và ∆FAD, có:
AF = AE (giả thiết).
\[\widehat {FAD} = \widehat {DAE}\] (AD là phân giác \[\widehat {BAC}\]).
AD là cạnh chung.
Do đó ∆EAD = ∆FAD (cạnh – góc – cạnh).
Suy ra \[\widehat {{E_2}} = \widehat {{F_2}}\].
Ta có \[\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ \] (hai góc kề bù).
Lại có \[\widehat {{F_1}} + \widehat {{F_2}} = 180^\circ \] (hai góc kề bù).
Do đó ta có \[\widehat {{E_1}} = \widehat {{F_1}}\] (1).
∆ABC vuông tại A: \[\widehat {ABC} + \widehat {ACB} = 90^\circ \].
∆CDE vuông tại D: \[\widehat {DEC} + \widehat {ACB} = 90^\circ \].
Do đó \[\widehat {ABC} = \widehat {DEC}\] hay \[\widehat {FBD} = \widehat {{E_1}}\] (2).
Từ (1), (2), ta suy ra \[\widehat {FBD} = \widehat {{F_1}}\].
Do đó ∆FBD cân tại D.
Vậy ta chọn đáp án C.
Câu 2
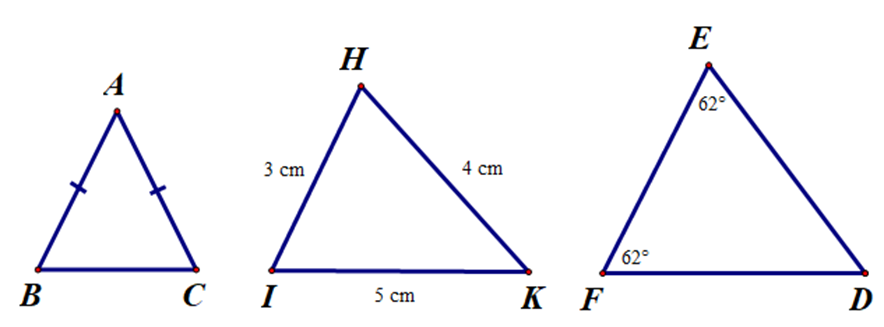
A. ∆DEF đều;
B. ∆DEF là tam giác vuông tại D;
C. ∆DEF là tam giác vuông cân tại F;
D. ∆DEF là tam giác vuông tại E.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
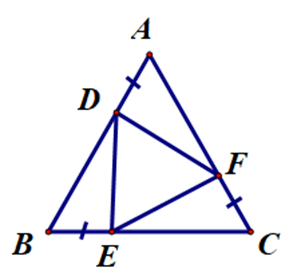
Vì ba điểm A, D, B thẳng hàng nên BD = AB – AD.
Vì ba điểm A, F, C thẳng hàng nên AF = AC – CF.
Ta có AB = AC (∆ABC đều) và AD = CF (giả thiết).
Do đó AB – AD = AC – CF.
Suy ra BD = AF.
Xét ∆ADF và ∆BED, có:
AD = BE (giả thiết).
BD = AF (chứng minh trên).
Do đó ∆ADF = ∆BED (cạnh – góc – cạnh).
Suy ra \[\widehat {FDA} = \widehat {DEB}\] (cặp góc tương ứng).
Xét ∆BDE, có: \[\widehat {BDE} + \widehat {EBD} + \widehat {DEB} = 180^\circ \].
Suy ra \[\widehat {BDE} + 60^\circ + \widehat {FDA} = 180^\circ \] (∆ABC đều).
Mà \[\widehat {BDE} + \widehat {EDF} + \widehat {FDA} = 180^\circ \] (kề bù).
Do đó \[\widehat {EDF} = 60^\circ \].
Chứng minh tương tự, ta được \[\widehat {DEF} = 60^\circ \].
Ta suy ra ∆DEF đều.
Do đó đáp án A đúng.
∆DEF là tam giác đều nên ∆DEF không thể là tam giác vuông (vì tam giác đều có các góc bằng nhau và cùng bằng 60°).
Do đó ta loại đáp án B, C, D.
Vậy ta chọn đáp án A.
Câu 3
A. ∆IBC là tam giác cân tại I;
B. ∆IBC là tam giác cân tại B;
C. ∆IBC là tam giác cân tại C;
D. ∆IBC là tam giác đều.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. ∆AMN cân tại A;
B. ∆AMN cân tại M;
C. ∆AMN cân tại N;
D. ∆AMN cân tại B.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
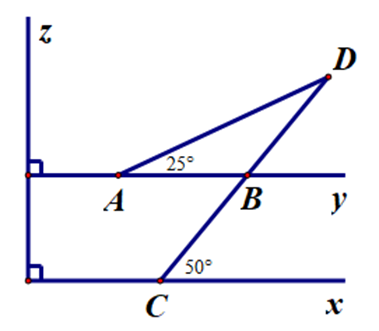
A. ∆ACD;
B. ∆ABD;
C. ∆BCD;
D. Hình vẽ bên không có tam giác nào cân.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. ∆ABC là tam giác cân tại A;
B. ∆ABC là tam giác cân tại B;
C. ∆ABC là tam giác là cân tại C;
D. ∆ABC là tam giác đều.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập