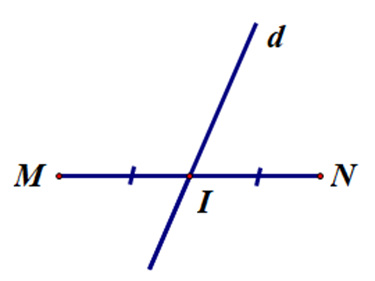Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
A. \[\widehat {ADC} = \widehat {ACD}\];
B. AK ⊥ DC;
C. AK là đường trung trực của đoạn thẳng DC;
D. Cả A, B, C đều đúng.
Quảng cáo
Trả lời:
Đáp án đúng là: D
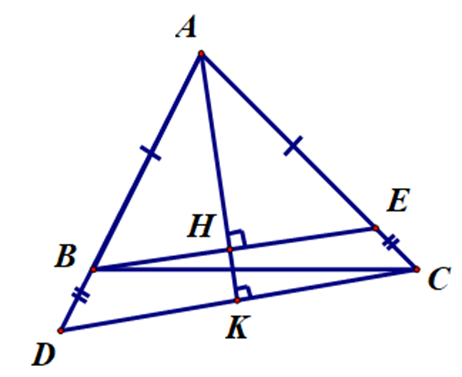
Vì AB = AE (giả thiết).
Nên ∆ABE cân tại A.
Suy ra \[\widehat {ABE} = \widehat {AEB}\].
∆ABE có: \[\widehat {BAC} + \widehat {ABE} + \widehat {AEB} = 180^\circ \].
Suy ra \[2\widehat {ABE} = 180^\circ - \widehat {BAC}\] (1).
Vì ba điểm A, B, D thẳng hàng và B nằm giữa A, D nên AD = AB + BD.
Vì ba điểm A, E, C thẳng hàng và E nằm giữa A, C nên AC = AE + EC.
Mà AB = AE và BD = EC (giả thiết).
Do đó AD = AC.
Suy ra ∆ADC cân tại A.
Khi đó ta có \[\widehat {ADC} = \widehat {ACD}\].
Do đó đáp án A đúng.
∆ADC có: \[\widehat {BAC} + \widehat {ADC} + \widehat {ACD} = 180^\circ \].
Suy ra \[2\widehat {ADC} = 180^\circ - \widehat {BAC}\] (2).
Từ (1), (2), ta suy ra \[\widehat {ADC} = \widehat {ABE}\].
Mà hai góc này ở vị trí đồng vị.
Do đó BE // DC.
Lại có AH ⊥ BE (giả thiết).
Suy ra AH ⊥ DC hay AK ⊥ DC (*).
Do đó đáp án B đúng.
Xét ∆ADK và ∆ACK, có:
AK là cạnh chung.
AD = AC (chứng minh trên).
\[\widehat {AKD} = \widehat {AKC} = 90^\circ \] (chứng minh trên).
Do đó ∆ADK = ∆ACK (cạnh huyền – cạnh góc vuông).
Suy ra DK = CK (cặp cạnh tương ứng).
Do đó K là trung điểm DC (**).
Từ (*), (**), ta suy ra AK là đường trung trực của đoạn thẳng DC.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. AD vuông góc với BC;
B. AD vuông góc với BE;
C. AD là đường trung trực của đoạn thẳng BE;
D. AD đi qua trung điểm của đoạn thẳng BE.
Lời giải
Đáp án đúng là: C
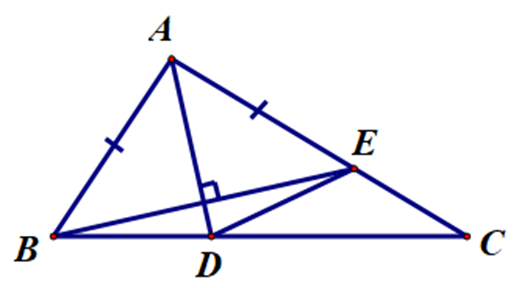
Xét ∆ABD và ∆AED, có:
AD là cạnh chung.
\[\widehat {BAD} = \widehat {EAD}\] (AD là phân giác của \[\widehat {BAC}\]).
AB = AE (giả thiết).
Do đó ∆ABD = ∆AED (cạnh – góc – cạnh).
Suy ra BD = ED.
Mà AB = AE (giả thiết).
Do đó AD là đường trung trực của đoạn thẳng BE.
Vì AD là đường trung trực của đoạn thẳng BE nên AD vừa vuông góc với BE, vừa đi qua trung điểm của đoạn thẳng BE.
Do đó đáp án C đúng nhất.
Với E ∈ AC, ta có AB = AE (giả thiết) và AB < AC (giả thiết).
Do đó AE < AC.
Suy ra ba điểm B, E, C không thẳng hàng.
Mà AD vuông góc với BE.
Nên AD không vuông góc với BC.
Do đó đáp án A sai.
Vậy ta chọn đáp án C.
Lời giải
Đáp án đúng là: A
Một đường thẳng là đường trung trực của một đoạn thẳng khi thỏa mãn cả hai yếu tố sau:
+ Đi qua trung điểm của đoạn thẳng.
+ Vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
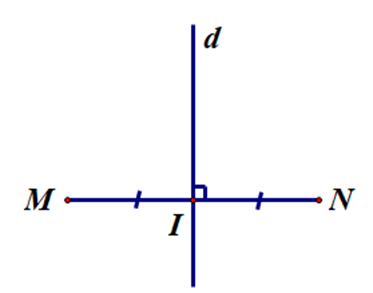
- Đường thẳng d ở đáp án A có đi qua trung điểm I của đoạn thẳng AB và vuông góc với đoạn thẳng MN tại trung điểm I.
Do đó đường thẳng d ở đáp án A là đường trung trực của đoạn thẳng MN.
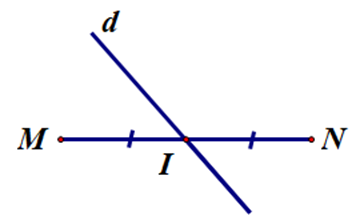
- Đường thẳng d ở đáp án B, D có đi qua trung điểm I nhưng không vuông góc với đoạn thẳng MN tại trung điểm I.
Do đó đường thẳng d ở đáp án B, D không là đường trung trực của đoạn thẳng MN.
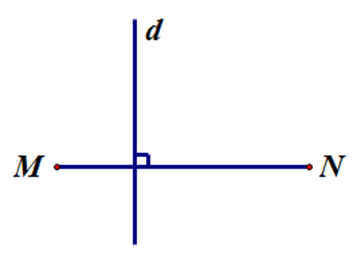
- Đường thẳng d ở đáp án C không đi qua trung điểm của đoạn thẳng MN.
Do đó đường thẳng d ở đáp án C không là đường trung trực của đoạn thẳng MN.
Vậy ta chọn đáp án A.
Câu 3
A. OH là đường trung trực của đoạn thẳng AB;
B. OC > OD;
C. OH là đường trung trực của đoạn thẳng CD;
D. OA = OB.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. AM là đường trung trực của đoạn thẳng BC;
B. AN là đường trung trực của đoạn thẳng BC;
C. MN là đường trung trực của đoạn thẳng BC;
D. Cả A, B, C đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. K thuộc đường trung trực của EF;
B. K thuộc đường trung trực của PQ;
C. DK là đường trung trực của EF;
D. DK không là đường trung trực của PQ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.Ot vuông góc với AB;
B.Ot là đường trung trực của đoạn thẳng AB;
C. Ot đi qua trung điểm của AB;
D. \[\widehat {OAI} \ne \widehat {OBI}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.