Cho hình tứ diện ABCD có tất cả các cạnh bằng 6a. Gọi M, N lần lượt là trung điểm của CA, CB. P là điểm trên cạnh BD sao cho BP = 2PD. Diện tích S thiết diện của tứ diện ABCD bị cắt bởi (MNP) là
A. S =
B. S =
C. S =
D. S =
Quảng cáo
Trả lời:
Chọn D.
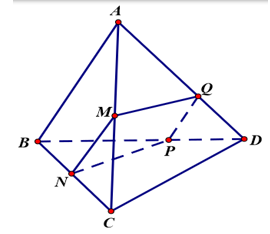
Trong mặt phẳng (ABD) qua P kẻ đường thẳng song song AB cắt AD tại Q, ta có
![]()
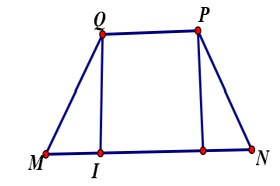
Dễ thấy MN là đường trung bình của tam giác ABC nên MN//AB//PQ, nên 4 điểm M, N, P, Q đồng phẳng MNPQ và MN = 3a, thiết diện cần tìm chính là hình thang MNPQ là hình thang cân, ta có
![]()
![]()
Kẻ đường cao QI ta có:
![]()
![]()
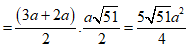
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. V =
B. V =
C. V =
D. V =
Lời giải
Chọn A.
![]()
Gọi ![]()
![]()
![]()
![]()
Lời giải
Chọn B.
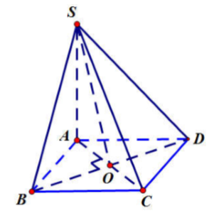
Gọi O = ACBD. Vì ABCD là hình thoi nên BOAC(1). Lại do:
![]()
Từ (1) và (2) ta có:BO(SAC)
![]()
Ta có: ![]()
Vì ABCD là hình thoi có ABC = 60 nên tam giác ABC đều cạnh a
![]()
Trong tam giác vuông SBO ta có:
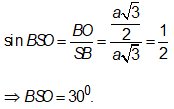
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.