Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = a. Biết SA = a và vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (SCD) bằng , với cos = . Tính theo a thể tích của khối chóp S.ABCD
A.
B.
C.
D.
Quảng cáo
Trả lời:
Chọn B.
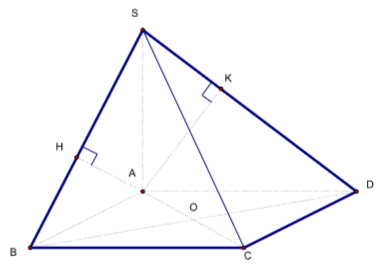
+ Gọi AD = x (x > 0)
+ Kẻ![]() dễ dàng chứng minh được
dễ dàng chứng minh được ![]()
![]()
Trong tam giác SBC ta có
![]()
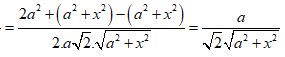
Trong tam giác SAD có ![]()
Xét tam giác AHK có
![]()
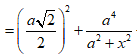
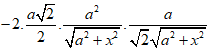
![]()
Xét tam giác AHK có
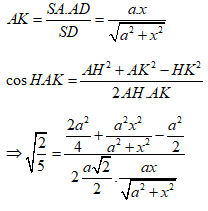
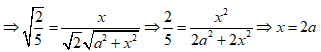
Vậy ![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. V =
B. V =
C. V =
D. V =
Lời giải
Chọn A.
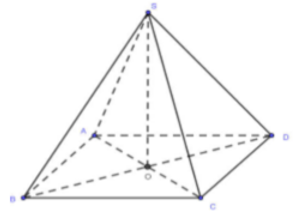
![]()
Gọi ![]()
![]()
![]()
![]()
Lời giải
Chọn B.
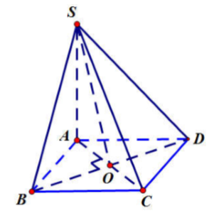
Gọi O = ACBD. Vì ABCD là hình thoi nên BOAC(1). Lại do:
![]()
Từ (1) và (2) ta có:BO(SAC)
![]()
Ta có: ![]()
Vì ABCD là hình thoi có ABC = 60 nên tam giác ABC đều cạnh a
![]()
Trong tam giác vuông SBO ta có:
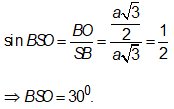
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.