Câu hỏi:

13/07/2024 1,757

Cho a, b, c là các số dương thỏa mãn (a + b + c)abc = 1. Tìm giá trị nhỏ nhất của biểu thức P = $\frac{a^{5}}{a^{3} + 2 b^{3}} + \frac{b^{5}}{b^{3} + 2 c^{3}} + \frac{c^{5}}{c^{3} + 2 a^{3}}$ .

Xem lời giải

Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có:

$\frac{a^{5}}{a^{3} + 2 b^{3}} = \frac{a^{2} [a^{3} + 2 b^{3}] - 2 a^{2} b^{3}}{a^{3} + 2 b^{3}}$ = a² − 2 $\frac{a^{2} b^{3}}{a^{3} + 2 b^{3}}$

a³ + 2b³ = a³ + b³ + b³ ≥ $3 \sqrt[3]{a^{3} . b^{3} . b^{3}}$ Þ a³ + 2b³≥ 3ab²

Þ $\frac{a^{2} b^{3}}{a^{3} + 2 b^{3}}$ ≤ $\frac{a^{2} b^{3}}{3 a b^{2}}$ Þ $\frac{a^{2} b^{3}}{a^{3} + 2 b^{3}}$ ≤ $\frac{a b}{3}$

Þ a² − 2 $\frac{a^{2} b^{3}}{a^{3} + 2 b^{3}}$ ≥ a² − $\frac{2}{3}$ ab Þ $\frac{a^{5}}{a^{3} + 2 b^{3}}$ ≥ a² − $\frac{2}{3}$ ab

Chứng minh tương tự

$\frac{b^{5}}{b^{3} + 2 c^{3}}$ ≥ b² − $\frac{2}{3}$ bc, $\frac{c^{5}}{c^{3} + 2 a^{3}}$ ≥ c² − $\frac{2}{3}$ ca.

Từ đây ta có S ≥ a² + b² + c² − $\frac{2}{3}$ ab − $\frac{2}{3}$ bc − $\frac{2}{3}$ ca

= $\frac{1}{2}$ [(a – b)² + (b – c)² + (c – a)²] + $\frac{1}{3}$ (ab + bc + ca)

Þ P ≥ $\frac{1}{3}$ (ab + bc + ca)

Áp dụng bất đẳng thức (x + y + z)² ≥ 3(xy + yz + zx), ta có:

(ab + bc + ca)² ≥ 3 Þ ab + bc + ca ≥ $\sqrt{3}$

Þ P ≥ $\frac{\sqrt{3}}{3}$ . Đẳng thức xảy ra khi và chỉ khi a = b = c = $\frac{1}{\sqrt[4]{3}}$

Vậy min S =

\frac{\sqrt{3}}{3}

tại (a;b;c) =

(\frac{1}{\sqrt[4]{3}}; \frac{1}{\sqrt[4]{3}}; \frac{1}{\sqrt[4]{3}})

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Bán kính đường tròn nội tiếp hình vuông có cạnh bằng a là

A. $a \sqrt{2}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a}{2}$

Lời giải

Đáp án đúng là: D

Bán kính đường tròn nội tiếp hình vuông có cạnh bằng a là (ảnh 1)

Gọi O là tâm của hình vuông ABCD, E; F; K; G lần lượt là trung điểm của AD, DC, BC, AB.

Khi đó ta có OE = OF = OK = OG = $\frac{a}{2}$ . Hay O là tâm đường tròn nội tiếp hình vuông ABCD.

Vậy bán kính đường tròn nội tiếp hình vuông là R = $\frac{a}{2}$ .

Câu 2

Bán kính đường tròn ngoại tiếp hình vuông có cạnh bằng 8cm là

\sqrt{2}

cm.

B. 8

\sqrt{2}

cm.

C. 4 cm.

D. 4

\sqrt{2}

cm.

Lời giải

Đáp án đúng là: D

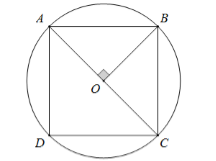
Bán kính đường tròn ngoại tiếp hình vuông có cạnh bằng 8cm là (ảnh 1)

Hình vuông ABCD nội tiếp đường tròn (O), O là tâm của hình vuông ABCD.

Vì ABCD là hình vuông nên 2 đường chéo vuông góc với nhau đồng thời chúng bằng nhau và cắt nhau tại trung điểm của mỗi đường Þ OA ^ OB và OA = OB.

Þ ∆OAB vuông cân tại O.

Gọi R là bán kính của đường tròn ngoại tiếp (O), ta có

AC = AB $\sqrt{2}$ = 8 $\sqrt{2}$ Þ R = $\frac{A B}{\sqrt{2}}$ = $\frac{8}{\sqrt{2}}$ = $4 \sqrt{2}$ cm.

Câu 3

Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao BD và CE của tam giác ABC cắt nhau tại H.

1) Tính $\hat{B D C}$ .

2) Chứng minh AEHD là tứ giác nội tiếp.

3) Các đường thẳng BD và CE cắt đường tròn (O) theo thứ tự tại P và Q (P khác B, Q khác C). Chứng minh HB.HP = HC.HQ.

4) Chứng minh OA vuông góc DE.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tứ giác ABCD nội tiếp đường tròn, khẳng định nào sau đây là đúng?

\hat{A B C} + \hat{B C D}

= 180°

\hat{A B C} + \hat{A D C}

= 120°.

C. $\hat{A B C} + \hat{A D C}$ = 180°.

\hat{A B C} + \hat{A D C}

= 90°.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số y = f(x) = x²

1) Tính f(−1); f(3).

2) Cho A(−1; 1), B(3; 9) nằm trên đồ thị hàm y = x². Gọi M là điểm thay đổi trên đồ thị hàm số y = x² và có hoành độ là m (−1 < m < 3). Tìm m để tam giác ABM có diện tích lớn nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cặp số (x; y) nào sau đây là nghiệm phương trình x – 5y = −7?

A. (2; 4).

B. (0; 1).

C. (3; 2).

D. (−1; 2).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Phương trình bậc hai x² + 2x – 3 = 0 có tổng hai nghiệm là

A. −2.

B. 1.

C. 2.

D. −1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho a, b, c là các số dương thỏa mãn (a + b + c)abc = 1. Tìm giá trị nhỏ nhất của biểu thức P = a5a3+2b3+b5b3+2c3+c5c3+2a3.

Bán kính đường tròn nội tiếp hình vuông có cạnh bằng a là

Bán kính đường tròn ngoại tiếp hình vuông có cạnh bằng 8cm là

Cho tứ giác ABCD nội tiếp đường tròn, khẳng định nào sau đây là đúng?

Cặp số (x; y) nào sau đây là nghiệm phương trình x – 5y = −7?

Phương trình bậc hai x2 + 2x – 3 = 0 có tổng hai nghiệm là

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho a, b, c là các số dương thỏa mãn (a + b + c)abc = 1. Tìm giá trị nhỏ nhất của biểu thức P = $\frac{a^{5}}{a^{3} + 2 b^{3}} + \frac{b^{5}}{b^{3} + 2 c^{3}} + \frac{c^{5}}{c^{3} + 2 a^{3}}$ .

Phương trình bậc hai x² + 2x – 3 = 0 có tổng hai nghiệm là