Trong hình vuông ABCD và nữa đường tròn đường kính AD và vẽ cung AC mà tâm là D. Nối D với điểm P bất kỳ trên cung AC, DP cắt nữa đường tròn đường kính AD ở K. Chứng minh PK bằng khoảng cách từ P đến AB.
Trong hình vuông ABCD và nữa đường tròn đường kính AD và vẽ cung AC mà tâm là D. Nối D với điểm P bất kỳ trên cung AC, DP cắt nữa đường tròn đường kính AD ở K. Chứng minh PK bằng khoảng cách từ P đến AB.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Cách giải 1: (Hình 1)
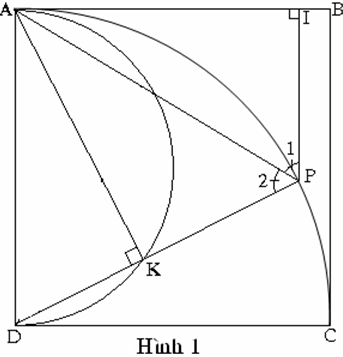
Kẻ PI AB.
Xét APK và API :
APK vuông tại K (Vì góc nội tiếp chắn nữa đường tròn đường kính AD)
ADP cân tại D, AD = DP
=>
Mặt khác: (So le trong vì AD // PI)
Do đó: => APK = API (Có chung cạnh huyền và một cặp góc nhọn bằng nhau) PK = PI
(Hình 2)
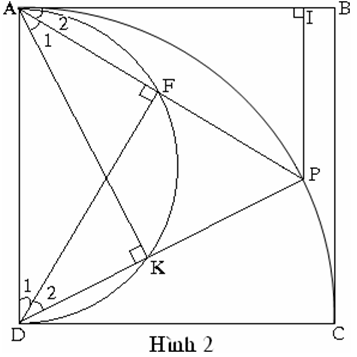
Ta có: (Góc nội tiếp chắn nữa đường tròn)
Tam giác ADP cân tại D có DF là đường cao nên DF cũng là phân giác suy ra
mà ; Vì đều là góc có các cặp cạnh tương ứng vuông góc
Suy ra: => APK = API (Có chung cạnh huyền và một cặp góc nhọn bằng nhau) PK = PI
Cách giải 3: (Hình 2)
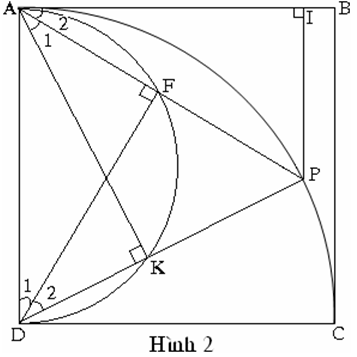
Ta có (Có số đo bằng sđ )
Mặt khác góc là góc tạo bởi tiếp tuyến và dây cung AP của đường tròn tâm D nên góc bằng nửa số đo của góc ở tâm cùng chắn một cung là góc
Suy ra: => APK = API
(Có chung cạnh huyền và một cặp góc nhọn bằng nhau) => PK = PI
Cách giải 4: (Hình 3)
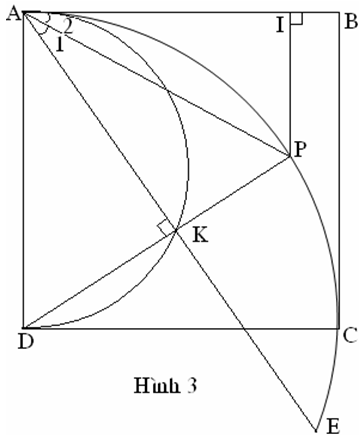
DK AE nên .
Góc (góc tạo bởi tiếp tuyến và dây cung )Vì AP lại đi qua điểm chính giữa của cung AE nên AP là tia phân giác của góc
Suy ra: => APK = API (Có chung cạnh huyền và một cặp góc nhọn bằng nhau) PK = PI
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập