Câu hỏi:

13/07/2024 2,376

Cho tam giác ABC, $\overset{⏞}{A} = 75 °$ ; $\overset{⏞}{B} = 60 °$ . Trên nửa mặt phẳng bờ BC có chứa A vẽ các tia Cx và Cy sao cho ACx=75 $°$ ; BCy=120 $°$ . Chứng tỏ rằng các tia Cx và Cy trùng nhau.

Hình 4.5

Xem lời giải

Câu hỏi trong đề: Bài tập chuyên đề Toán 7 Dạng 1: Tiên đề Ơ-clit. Tính chất của hai đường thằng song song có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có ACx = $\overset{⏞}{A}$ =75 $°$ => Cx // AB(vì có cặp góc so le trong bằng nhau). (1)

Ta có BCy + $\overset{⏞}{B}$ =120 $°$ +60 $°$ = 180 $°$

=> Cy // AB (vì có cặp góc trong cùng phía bù nhau). (2)

Từ (1) và (2), theo tiên đề Ơ-clít, ta có hai đường thẳng Cx và Cy trùng nhau. Mặt khác, hai tia Cx và Cy cùng nằm trên một nửa mặt phẳng bờ BC có chứa A nên hai tia này trùng nhau.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong hình 4.18 có Ax // By. Tính số đo của góc AOB.

Xem đáp án

Lời giải

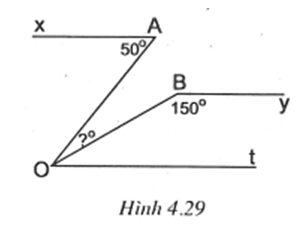
Trong hình 4.18 có Ax // By. Tính số đo của góc AOB. (ảnh 2)

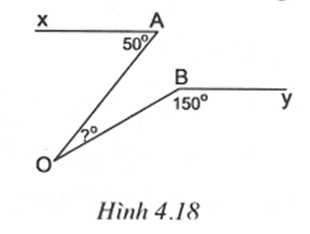
Trên nửa mặt phẳng bờ OB có chứa tia By vẽ tia Ot // By. Khi đó Ot // Ax.

Ta có $\overset{⏞}{O B y} + \overset{⏞}{B O t} = 180 °$ (cặp góc trong cùng phía).

Suy ra BOt = 30 $°$ .

Ta có $\overset{⏞}{A O t} = \overset{⏞}{O A x} = 50 °$ (cặp góc so le trong).

Từ đó $\overset{⏞}{A O B} = 20 °$ .

Câu 2

Hình 4.17 có Ax // By; OA $⊥ O B$ và $\overset{⏞}{A} = 145 °$ . Tính số đo góc B.

Xem đáp án

Lời giải

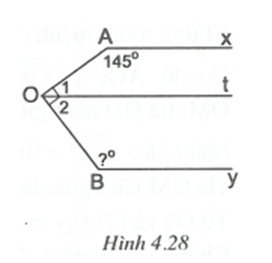
Hình 4.17 có Ax // By; OA và . Tính số đo góc B. (ảnh 2)

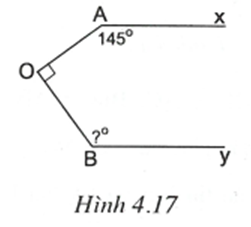
trong góc AOB vẽ tia Ot // Ax.

Khi đó Ot // By.

Ta có $O A ⊥ O B$ nên $\overset{⏞}{A O B} = 90 °$ .

Mặt khác $\overset{⏞}{A} + \overset{⏞}{O_{1}} = 180 °$ (cặp góc trong cùng phía) nên $\overset{⏞}{O_{1}} = 35 °$ .

Suy ra $\overset{⏞}{O_{2}} = 55 °$ .

Ta có $\overset{⏞}{O_{2}} + \overset{⏞}{B} = 180 °$ (cặp góc trong cùng phía của Ot // By).

Do đó $\overset{⏞}{B} = 125 °$ .

Câu 3

Cho tam giác ABC. Vẽ điểm M sao cho góc BAM bằng và so le trong với góc B. Vẽ điểm N sao góc CAN bằng và so le trong với góc C. Chứng tỏ rằng ba điểm M, A, N thẳng hàng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC. Từ điểm M trên cạnh BC vẽ MD//AB, ME//AC. Xác định vị trí của điểm M để tia MA là tia phân giác của góc DME.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tính các số đo x, y trong hình 4.6, biết $\overset{⏞}{A_{1}} = \overset{⏞}{A_{2}}; \overset{⏞}{B_{1}} = \overset{⏞}{B_{2}}$ và x= $\frac{3}{7} y$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho góc AOB. Trên tia OA lấy điểm M, trên tia OB lấy điểm N. Vẽ ra ngoài góc AOB các tia Mx và Ny song song với nhau. Cho biết $\overset{⏞}{A M x} = 140 °$ , $\overset{⏞}{B N y} = 150 °$ . tính số đo của góc AOB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho tam giác ABC, $\overset{⏞}{A} = 75 °$ ; $\overset{⏞}{B} = 60 °$ . Trên nửa mặt phẳng bờ BC có chứa A vẽ các tia Cx và Cy sao cho ACx=75 $°$ ; BCy=120 $°$ . Chứng tỏ rằng các tia Cx và Cy trùng nhau.

Hình 4.5

Hình 4.17 có Ax // By; OA $⊥ O B$ và $\overset{⏞}{A} = 145 °$ . Tính số đo góc B.

Tính các số đo x, y trong hình 4.6, biết $\overset{⏞}{A_{1}} = \overset{⏞}{A_{2}}; \overset{⏞}{B_{1}} = \overset{⏞}{B_{2}}$ và x= $\frac{3}{7} y$ .

Cho góc AOB. Trên tia OA lấy điểm M, trên tia OB lấy điểm N. Vẽ ra ngoài góc AOB các tia Mx và Ny song song với nhau. Cho biết $\overset{⏞}{A M x} = 140 °$ , $\overset{⏞}{B N y} = 150 °$ . tính số đo của góc AOB.