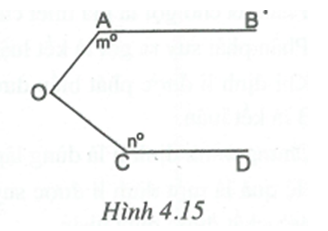
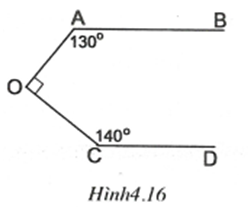
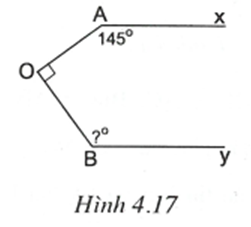
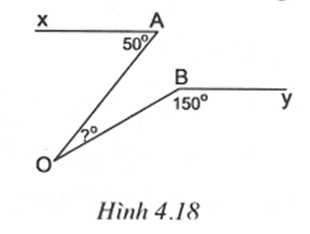
Bài tập chuyên đề Toán 7 Dạng 1: Tiên đề Ơ-clit. Tính chất của hai đường thằng song song có đáp án
44 người thi tuần này 4.6 3.5 K lượt thi 21 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu Trắc nghiệm Toán 7 Cánh diều Ôn tập chương VI (Đúng sai - Trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
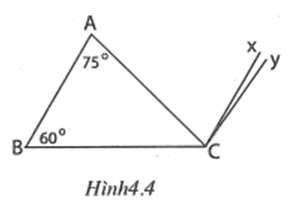
Ta có ACx = =75 => Cx // AB(vì có cặp góc so le trong bằng nhau). (1)
Ta có BCy + =120+60= 180
=> Cy // AB (vì có cặp góc trong cùng phía bù nhau). (2)
Từ (1) và (2), theo tiên đề Ơ-clít, ta có hai đường thẳng Cx và Cy trùng nhau. Mặt khác, hai tia Cx và Cy cùng nằm trên một nửa mặt phẳng bờ BC có chứa A nên hai tia này trùng nhau.
Lời giải
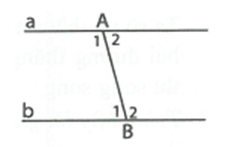
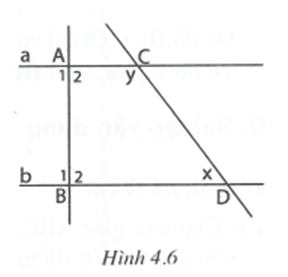
Ta có a // b nên (cặp góc trong cùng phía).
Mặt khác, (đề bài) nên và .
Suy ra (cặp góc so le trong); (cặp góc so le trong).
Lời giải
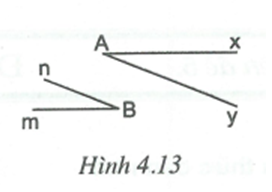
Ta có (kề bù) mà (đề bài) nên .
Suy ra AB .
Tương tự AB .
Do đó a // b (cùng vuông góc với AB).
Ta có x + y = 180 (cặp góc trong cùng phía) mà x= nên x= .
Lời giải
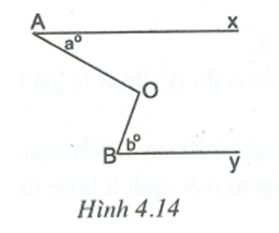
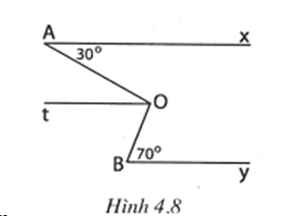
Ở trong góc AOB, vẽ tia Ot //Ax. Khi đó (cặp góc so le trong).
Suy ra .
Vậy .
Do đó By // Ot (vì có cặp so le trong bằng nhau).
Từ đó suy ra Ax // By (vì cùng song song với Ot).
Lời giải
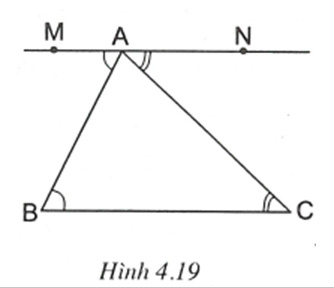
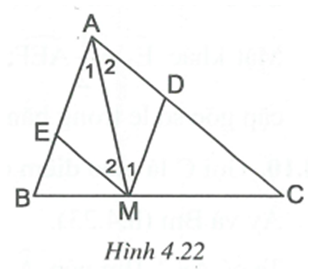
Ta có suy ra AM // BC (vì có cặp góc so le trong bằng nhau).
suy ra AN // BC (vì có cặp góc so le trong bằng nhau).
Theo tiên đề Ơ-clít qua điểm A chỉ có một đường thẳng song song với BC, do đó ba điểm M, A, N thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.