Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
37 người thi tuần này 5.0 3.5 K lượt thi 39 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. x + 3y = 7;
B. x2 + y2 = 5;
C. \(y = \sqrt {{x^2} - 2} \);
D. \(y = \frac{2}{x}\).
Lời giải
Đáp án B
Câu 2
A. 2
B. 3
C. 5
D. 7
Lời giải
Đáp án C
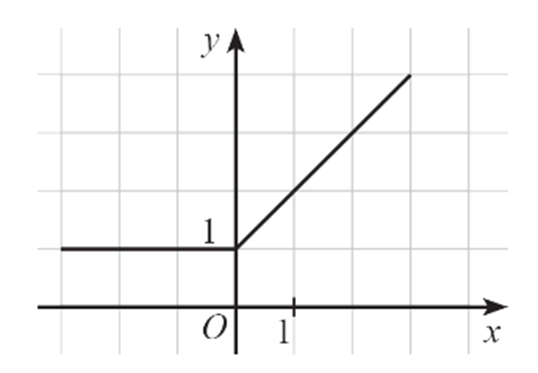
Câu 3
A. (0; 1);
B. (1; + ∞);
C. (0; + ∞);
D. (– ∞; 0).
Lời giải
Đáp án đúng là: C
Từ hình vẽ ta thấy đồ thị hàm số y = f(x) đi lên từ trái sang phải trên khoảng (0; + ∞). Vậy hàm số này đồng biến trên khoảng (0; + ∞).
Câu 4
A. (1; 2);
B. [1; 2];
C. {1; 2};
D. ℝ \ {1; 2}.
Lời giải
Đáp án đúng là: D
Biểu thức \(\frac{{x + 2}}{{{x^2} - 3x + 2}}\) có nghĩa khi x2 – 3x + 2 ≠ 0 ⇔ x ≠ 1 và x ≠ 2.
Vậy tập xác định của hàm số \(y = \frac{{x + 2}}{{{x^2} - 3x + 2}}\) là D = ℝ \ {1; 2}.
Câu 5
A. 20;
B. \(10\sqrt 2 \);
C. \[2\sqrt {10} \];
D. Không tồn tại.
Lời giải
Đáp án đúng là: B
Ta có: \(y\left( {10} \right) = 2\sqrt {{{10}^2} - 5.10} = 10\sqrt 2 \).
Câu 6
A. y = x2 – 5x + 3;
B. y = 1 – 2x2 + 4x;
C. y = x(x2 + x + 1);
D. y = 7 – x2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \( - \frac{3}{4}\);
B. \(\frac{3}{4}\);
C. \(\frac{3}{2}\);
D. \( - \frac{3}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. Hàm số đồng biến trên khoảng (– ∞; 2), nghịch biến trên khoảng (2; + ∞);
B. Hàm số đồng biến trên khoảng (– ∞; 4), nghịch biến trên khoảng (4; + ∞);
C. Hàm số đồng biến trên khoảng (4; + ∞), nghịch biến trên khoảng (– ∞; 4);
D. Hàm số đồng biến trên khoảng (2; + ∞), nghịch biến trên khoảng (– ∞; 2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. y = – x2 + 2;
B. y = x2 + 2;
C. y = 2x2 – 1;
D. y = 2x2 + 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. f(x) = 3x2 + x – 4 là tam thức bậc hai;
B. f(x) = 3x – 5 là tam thức bậc hai;
C. f(x) = 2x3 + 3x – 2 là tam thức bậc hai;
D. f(x) = (x2)2 – x2 + 3 là tam thức bậc hai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. ∆ ≤ 0;
B. ∆ = 0;
C. ∆ > 0;
D. ∆ < 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. Phương trình f(x) = 0 vô nghiệm;
B. f(x) > 0 với mọi x ∈ ℝ;
C. f(x) ≥ 0 với mọi x ∈ ℝ;
D. f(x) < 0 khi x < 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. x2 – 3x + 2 > 0 khi x ∈ (– ∞; 1) ∪ (2; + ∞);
B. x2 – 3x + 2 ≤ 0 khi x ∈ [1; 2];
C. x2 – 3x + 2 < 0 khi x ∈ [1; 2);
D. x2 – 3x + 2 ≥ 0 khi x ∈ (– ∞; 1] ∪ [2; + ∞).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập nghiệm của phương trình ax2 + bx + c = (dx + e)2;
B. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình dx + e ≥ 0;
C. Mọi nghiệm của phương trình ax2 + bx + c = (dx + e)2 đều là nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\];
D. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình ax2 + bx + c ≥ 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập nghiệm của phương trình ax2 + bx + c = dx2 + ex + f;
B. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập nghiệm của phương trình (ax2 + bx + c)2 = (dx2 + ex + f)2;
C. Mọi nghiệm của phương trình ax2 + bx + c = dx2 + ex + f đều là nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \];
D. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập hợp các nghiệm của phương trình ax2 + bx + c = dx2 + ex + f thỏa mãn bất phương trình ax2 + bx + c ≥ 0 (hoặc dx2 + ex + f ≥ 0).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. 2;
B. 4;
C. 12;
D. 20.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Vectơ pháp tuyến của đường thẳng d là
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Vectơ pháp tuyến của đường thẳng d là
A. \(\overrightarrow n = \left( {1;\,\, - 2} \right)\);
B. \(\overrightarrow n = \left( {1;\,\,2} \right)\);
C. \(\overrightarrow n = \left( {2;\,\, - 1} \right)\);
D. \(\overrightarrow n = \left( {2;\,\,1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. A(1; 2);
B. B(0; 2);
C. C(2; 0);
D. D(2; 1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = 1 - t\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = 1 + t\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 + t\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 - t\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. x – y + 2 = 0;
B. – 3x + y + 4 = 0;
C. x – 3y + 4 = 0;
D. x + 3y + 4 = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 2x + y – 1 = 0;
B. – 2x + y – 1 = 0;
C. x + 2y + 1 = 0;
D. 2x + 3y – 1 = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A. x + y – 3 = 0;
B. y = 2x + 2;
C. \(\frac{{x - 4}}{6} = \frac{{y - 1}}{{ - 4}}\);
D. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 - 2t\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. hệ (*) có vô số nghiệm;
B. hệ (*) vô nghiệm;
C. hệ (*) có nghiệm duy nhất;
D. hệ (*) có hai nghiệm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. \[d\left( {M,\,\,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\];
B. \[d\left( {M,\,\,\Delta } \right) = \frac{{a{x_0} + b{y_0} + c}}{{\sqrt {{a^2} + {b^2}} }}\];
C. \[d\left( {M,\,\,\Delta } \right) = \frac{{a{x_0} + b{y_0} + c}}{{\sqrt {x_0^2 + y_0^2} }}\];
D. \[d\left( {M,\,\,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {x_0^2 + y_0^2} }}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
A. \(\cos \varphi = \cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
B. \(\cos \varphi = - \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = - \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = - \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
C. \(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
D. \(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + a_2^2} \cdot \sqrt {b_1^2 + b_2^2} }}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. 13;
B. – 13;
C. – 1;
D. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
A. 2x2 + y2 – 6x – 6y – 8 = 0;
B. x2 + 2y2 – 4x – 8y – 12 = 0;
C. x2 + y2 – 2x – 8y + 18 = 0;
D. 2x2 + 2y2 – 4x + 6y – 12 = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. (x – 1)2 + (y + 2)2 = 25;
B. (x + 1)2 + (y + 2)2 = 25;
C. (x + 1)2 + (y – 2)2 = 25;
D. (x – 1)2 + (y – 2)2 = 25.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
A. (x – 3)2 + (y – 4)2 = 9;
B. (x + 3)2 + (y – 4)2 = 9;
C. (x – 3)2 + (y – 4)2 = 3;
D. (x + 3)2 + (y + 4)2 = 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
A. y = – 2;
B. x = 1;
C. x + 2y – 1 = 0;
D. x – 2y – 1 = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.