Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH. Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC).
a) Chứng minh tứ giác ADHE là hình chữ nhật.
b) Gọi I là trung điểm của đoạn thẳng HC. Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng AC // HK.
c) Chứng minh tứ giác DECK là hình thang cân.
d) Gọi O là giao điểm của DE và AH. Gọi M là giao điểm của AI và CO. Chứng minh \(AM = \frac{1}{3}AK\).
Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH. Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC).
a) Chứng minh tứ giác ADHE là hình chữ nhật.
b) Gọi I là trung điểm của đoạn thẳng HC. Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng AC // HK.
c) Chứng minh tứ giác DECK là hình thang cân.
d) Gọi O là giao điểm của DE và AH. Gọi M là giao điểm của AI và CO. Chứng minh \(AM = \frac{1}{3}AK\).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
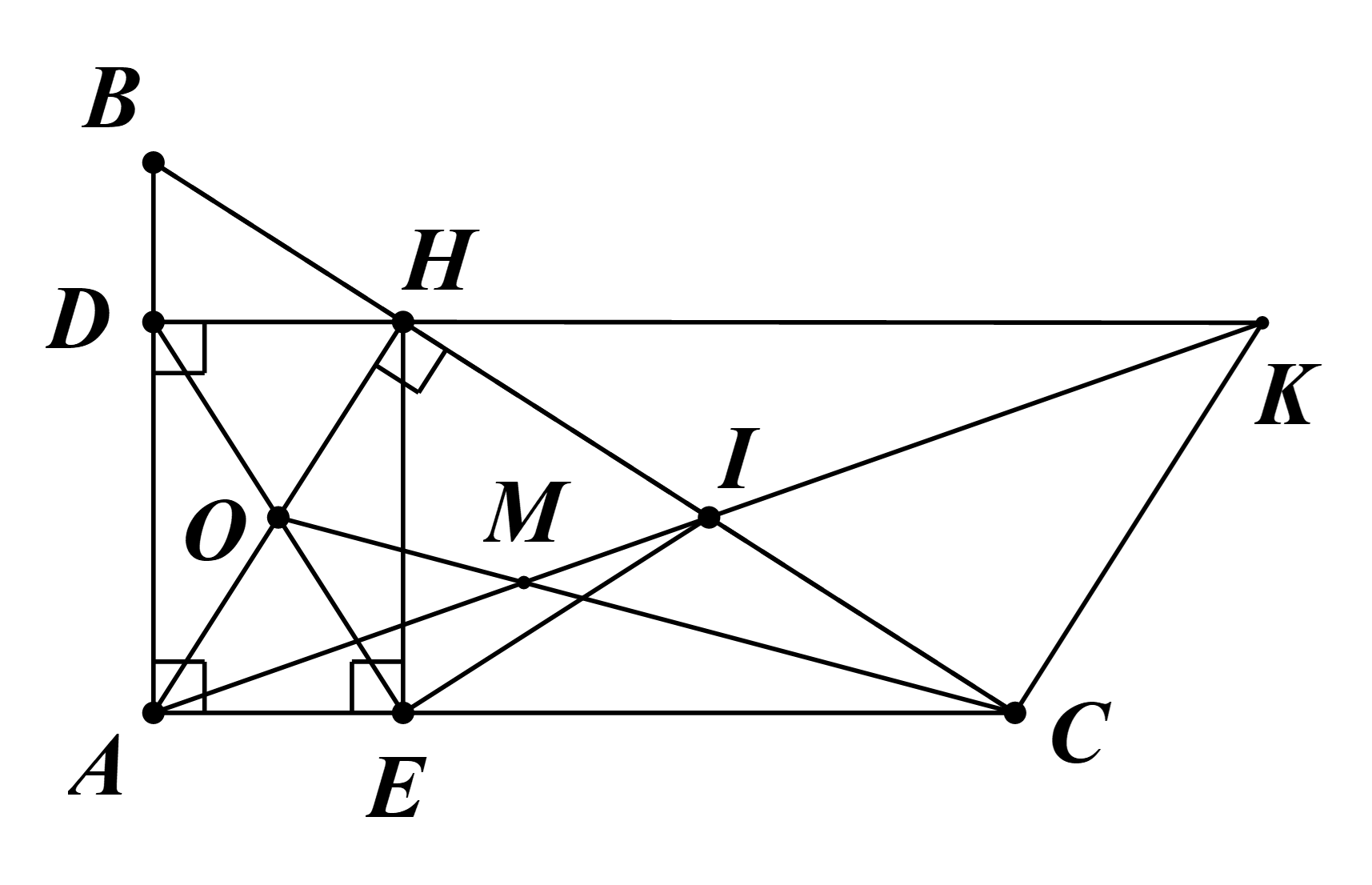
a) Tứ giác ADHE, có:
\[\widehat {DAE} = 90^\circ \] (do tam giác ABC vuông tại A);
\[\widehat {ADH} = 90^\circ \] (do HD ⊥ AB tại D);
\[\widehat {AEH} = 90^\circ \] (do HE ⊥ AC tại E).
Vậy tứ giác ADHE là hình chữ nhật.
b) Ta có K là điểm đối xứng của A qua I (giả thiết).
Suy ra I là trung điểm của AK.
Mà I cũng là trung điểm của HC (giả thiết).
Do đó tứ giác AHKC là hình bình hành.
Vậy AC // HK.
c) Xét ∆DHE và ∆AEH, có:
HE chung;
\(\widehat {DHE} = \widehat {AEH} = 90^\circ \);
DH = AE (ADHE là hình chữ nhật).
Do đó ∆DHE = ∆AEH (c.g.c).
Suy ra \(\widehat {HDE} = \widehat {HAE}\) (cặp cạnh tương ứng).
Mà \(\widehat {HKC} = \widehat {HAC}\) (do tứ giác AHKC là hình bình hành).
Do đó \(\widehat {HDE} = \widehat {HKC}\).
Mà AC // DK (chứng minh trên).
Vậy tứ giác DECK là hình thang cân.
d) Tam giác ACH có các đường trung tuyến AI, CO cắt nhau tại M.
Suy ra M là trọng tâm của tam giác ACH.
Do đó \(AM = \frac{2}{3}AI\).
Mà \(AI = \frac{1}{2}AK\) (do I là trung điểm AK).
Suy ra \(AM = \frac{2}{3}AI = \frac{2}{3}.\frac{1}{2}AK = \frac{1}{3}AK\).
Vậy \(AM = \frac{1}{3}AK\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
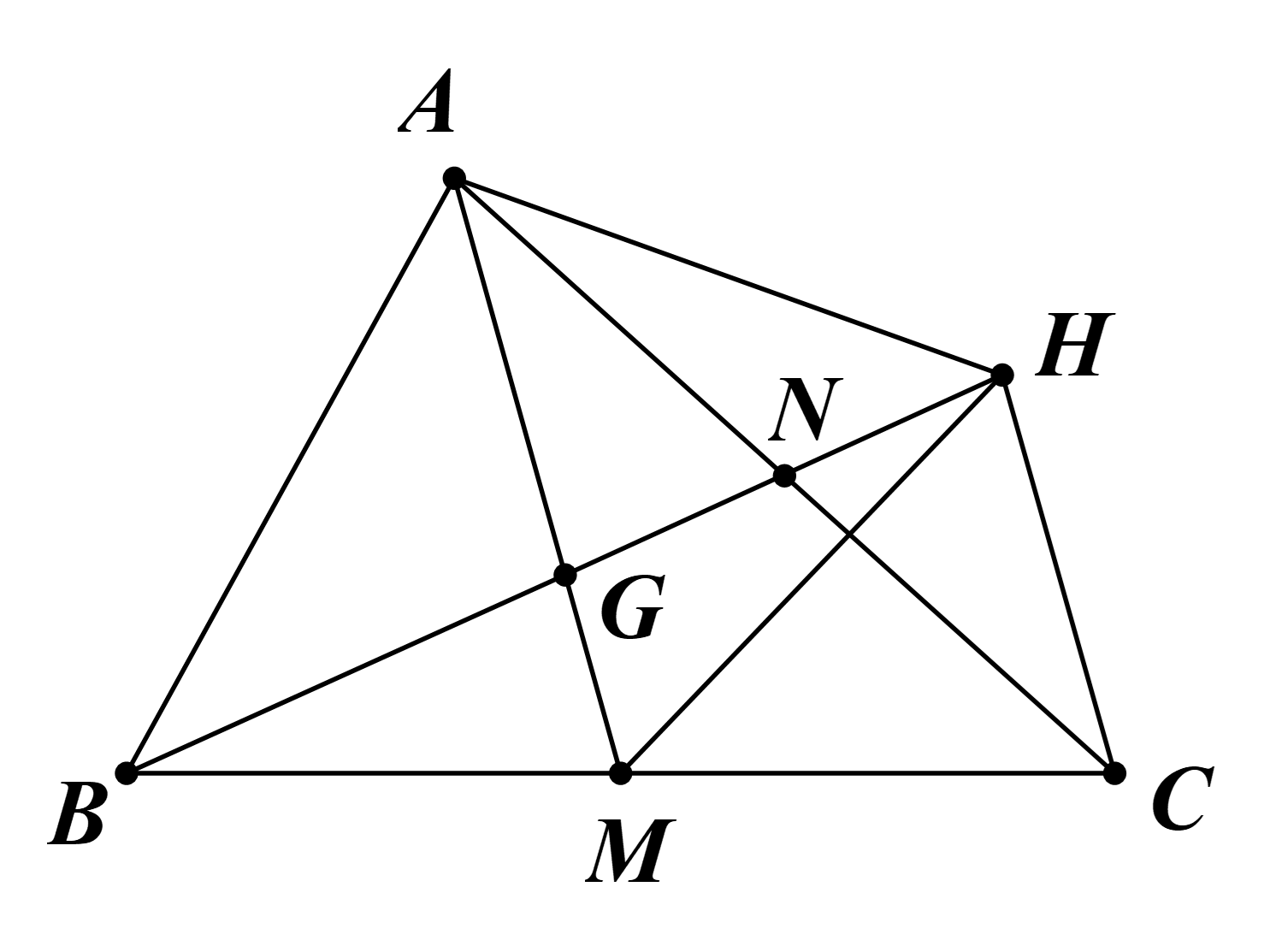
a) Gọi N là trung điểm AC.
Do H là điểm đối xứng của B qua G.
Suy ra G là trung điểm của BH.
Do đó \(GH = BG = \frac{2}{3}BN = 2GN\) (do G là trọng tâm tam giác ABC).
Vì vậy N là trung điểm GH (do 4 điểm B, G, N, H thẳng hàng).
Suy ra GN = NH.
Ta có \(\overrightarrow {AH} = \overrightarrow {AN} + \overrightarrow {NH} = \overrightarrow {AN} + \overrightarrow {GN} \)
\( = \overrightarrow {AN} + \frac{1}{3}\overrightarrow {BN} = \overrightarrow {AN} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)
\[ = \frac{4}{3}\overrightarrow {AN} - \frac{1}{3}\overrightarrow {AB} = \frac{4}{3}\left( {\frac{1}{2}\overrightarrow {AC} } \right) - \frac{1}{3}\overrightarrow {AB} \]
\[ = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \].
Ta có \(\overrightarrow {CH} = \overrightarrow {CN} + \overrightarrow {NH} = \overrightarrow {CN} + \overrightarrow {GN} \)
\( = \overrightarrow {CN} + \frac{1}{3}\overrightarrow {BN} = \overrightarrow {CN} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)
\[ = \overrightarrow {CN} - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AN} = - \frac{1}{2}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}.\frac{1}{2}\overrightarrow {AC} \]
\( = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \).
Vậy ta có điều phải chứng minh.
b) \(\overrightarrow {MH} = \overrightarrow {MB} + \overrightarrow {BH} = \frac{1}{2}\overrightarrow {CB} + \overrightarrow {BA} + \overrightarrow {AH} \)
\( = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AB} } \right) - \overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \)
\( = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Vậy ta có điều phải chứng minh.
Lời giải
Lời giải
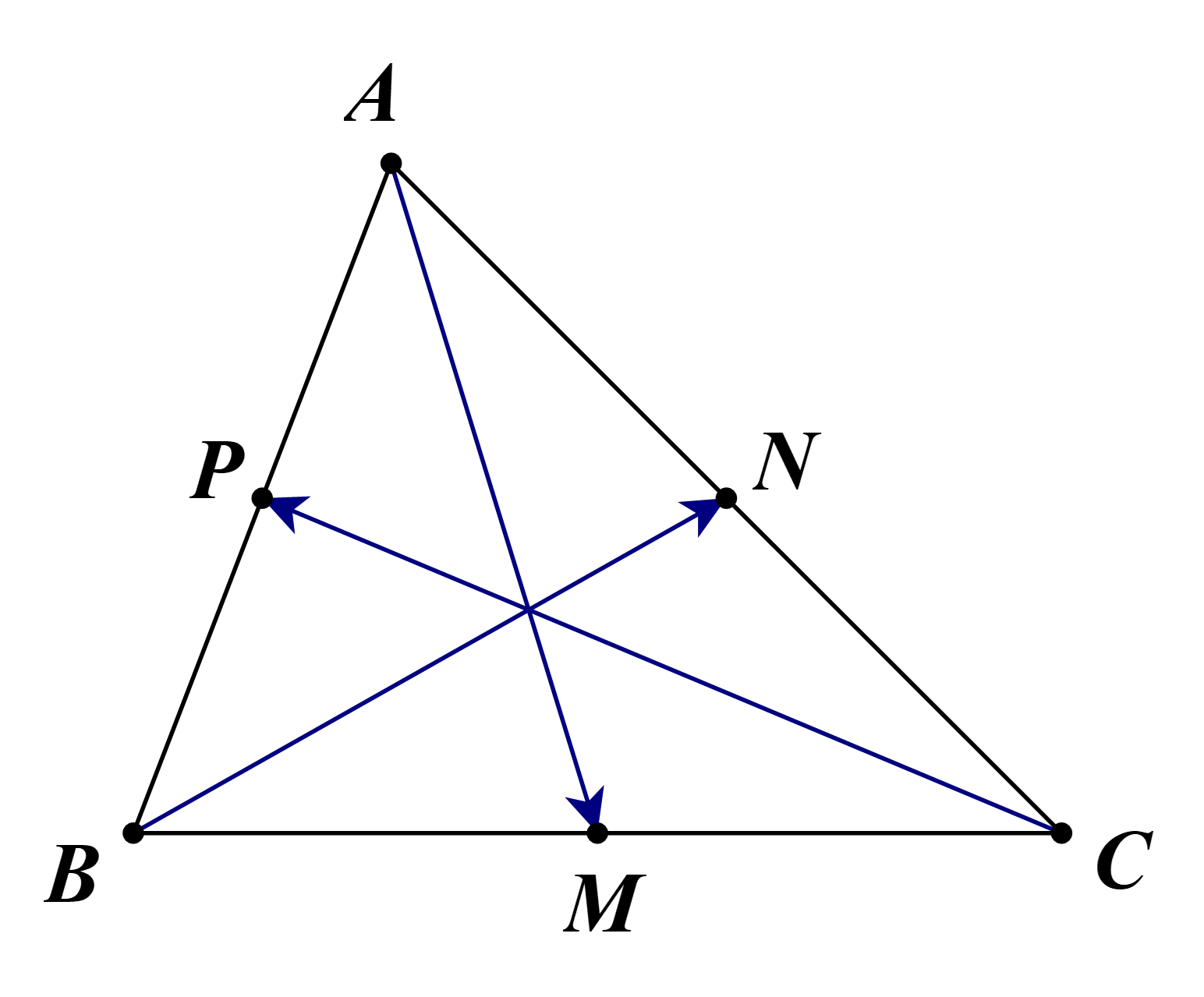
a) Ta có \(VT = \overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} \) (do M, N, P lần lượt là trung điểm của BC, CA, AB).
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BA} } \right) + \frac{1}{2}\left( {\overrightarrow {CB} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AC} } \right)\)
\( = \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 = \vec 0 = VP\).
Vậy ta có điều phải chứng minh.
b) Ta có \(VT = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\)
\( = \frac{1}{2}.2\overrightarrow {OP} + \frac{1}{2}.2\overrightarrow {ON} + \frac{1}{2}.2\overrightarrow {OM} \)
\( = \overrightarrow {OP} + \overrightarrow {ON} + \overrightarrow {OM} = VP\).
Vậy ta có điều phải chứng minh.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.