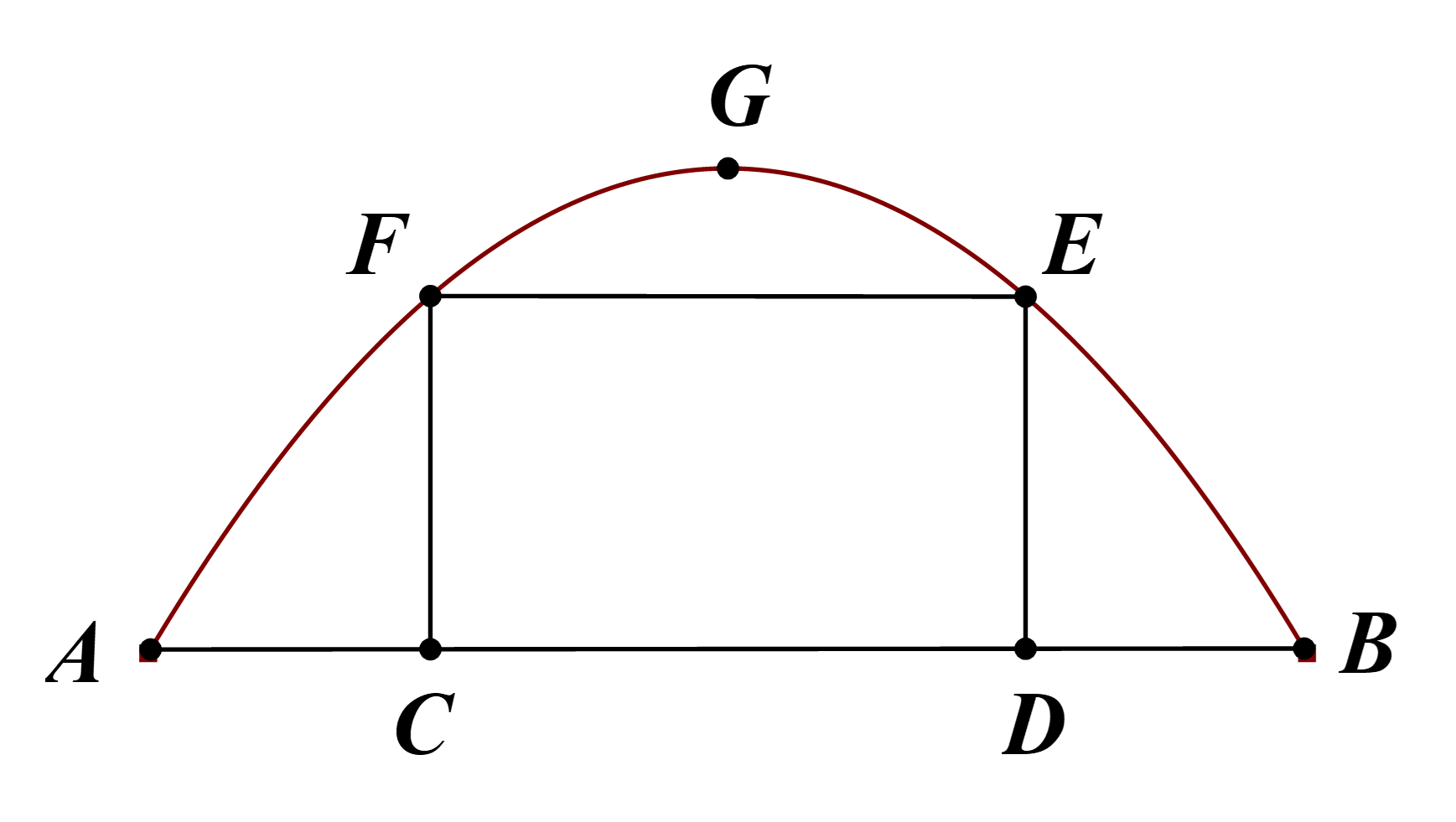
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4 m còn kích thước cửa ở giữa là 3 m x 6 m. Hãy tính khoảng cách giữa hai điểm A và B.

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
Chọn hệ trục tọa độ Oxy như hình vẽ.
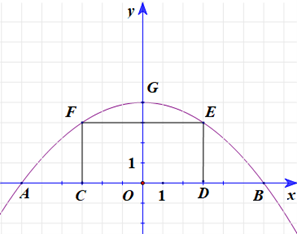
Phương trình parabol có dạng (P): y = ax2 + bx + c (a < 0).
Ta có G(0; 4) ∈ (P) ⇒ c = 4.
Theo đề, ta có kích thước cửa ở giữa là 3 m x 6 m.
Suy ra E(3; 3), F(–3; 3).
Ta có \(\left\{ \begin{array}{l}E \in \left( P \right)\\F \in \left( P \right)\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}9a + 3b + c = 3\\9a - 3b + c = 3\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}9a + 3b = - 1\\9a - 3b = - 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}18a = - 2\\b = \frac{{9a + 1}}{3}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{9}\\b = 0\end{array} \right.\)
So với điều kiện a < 0, ta nhận \(a = - \frac{1}{9}\).
Khi đó phương trình parabol (P): \(y = - \frac{1}{9}{x^2} + 4\).
Phương trình hoành độ giao điểm của (P) và trục Ox là: \( - \frac{1}{9}{x^2} + 4 = 0\)
⇔ x2 = 36
⇔ x = ±6.
Suy ra tọa độ A(–6; 0), B(6; 0).
Do đó AB = 12 m.
Vậy ta chọn phương án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
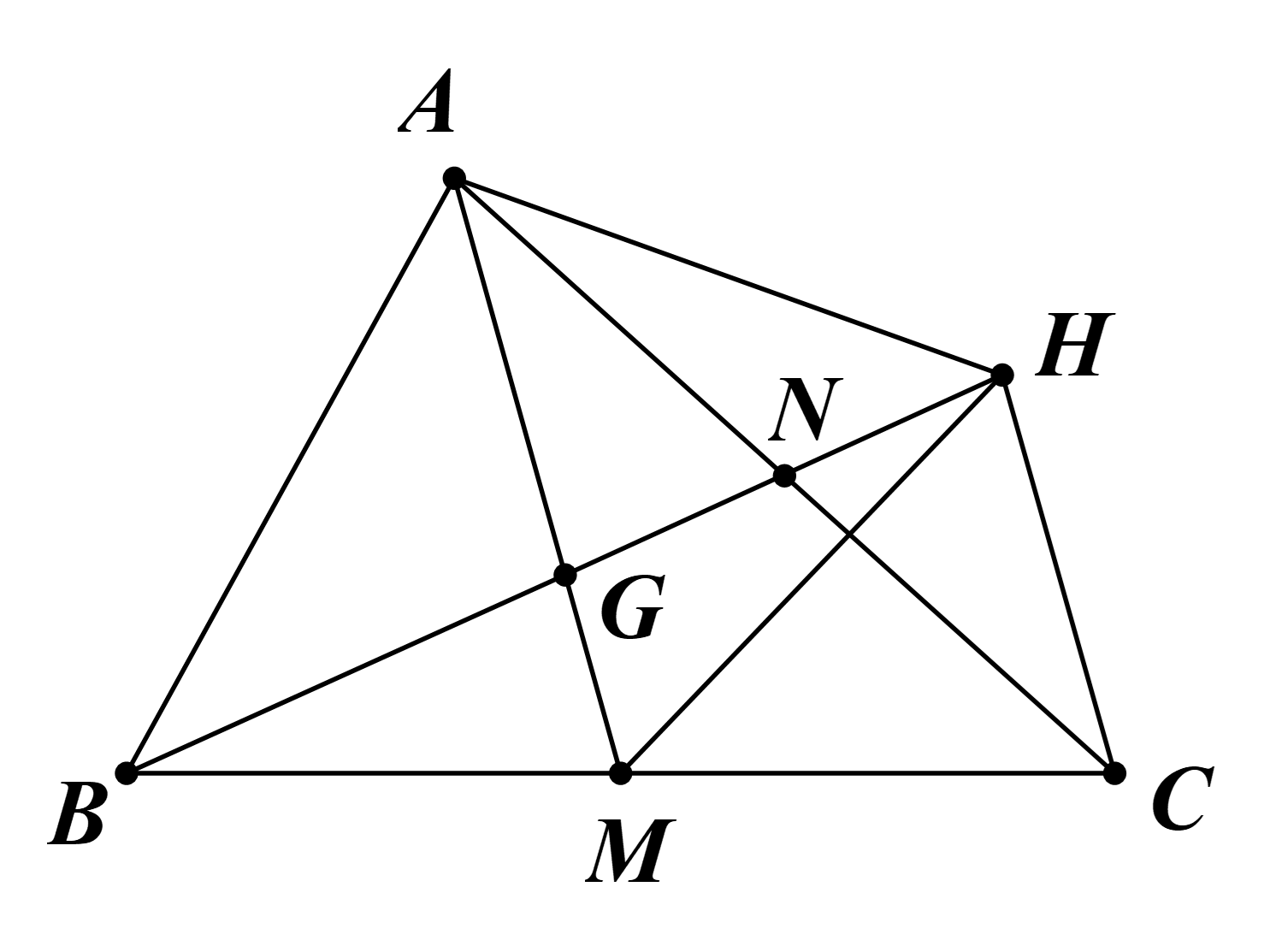
a) Gọi N là trung điểm AC.
Do H là điểm đối xứng của B qua G.
Suy ra G là trung điểm của BH.
Do đó \(GH = BG = \frac{2}{3}BN = 2GN\) (do G là trọng tâm tam giác ABC).
Vì vậy N là trung điểm GH (do 4 điểm B, G, N, H thẳng hàng).
Suy ra GN = NH.
Ta có \(\overrightarrow {AH} = \overrightarrow {AN} + \overrightarrow {NH} = \overrightarrow {AN} + \overrightarrow {GN} \)
\( = \overrightarrow {AN} + \frac{1}{3}\overrightarrow {BN} = \overrightarrow {AN} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)
\[ = \frac{4}{3}\overrightarrow {AN} - \frac{1}{3}\overrightarrow {AB} = \frac{4}{3}\left( {\frac{1}{2}\overrightarrow {AC} } \right) - \frac{1}{3}\overrightarrow {AB} \]
\[ = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \].
Ta có \(\overrightarrow {CH} = \overrightarrow {CN} + \overrightarrow {NH} = \overrightarrow {CN} + \overrightarrow {GN} \)
\( = \overrightarrow {CN} + \frac{1}{3}\overrightarrow {BN} = \overrightarrow {CN} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)
\[ = \overrightarrow {CN} - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AN} = - \frac{1}{2}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}.\frac{1}{2}\overrightarrow {AC} \]
\( = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \).
Vậy ta có điều phải chứng minh.
b) \(\overrightarrow {MH} = \overrightarrow {MB} + \overrightarrow {BH} = \frac{1}{2}\overrightarrow {CB} + \overrightarrow {BA} + \overrightarrow {AH} \)
\( = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AB} } \right) - \overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \)
\( = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Vậy ta có điều phải chứng minh.
Lời giải
Lời giải
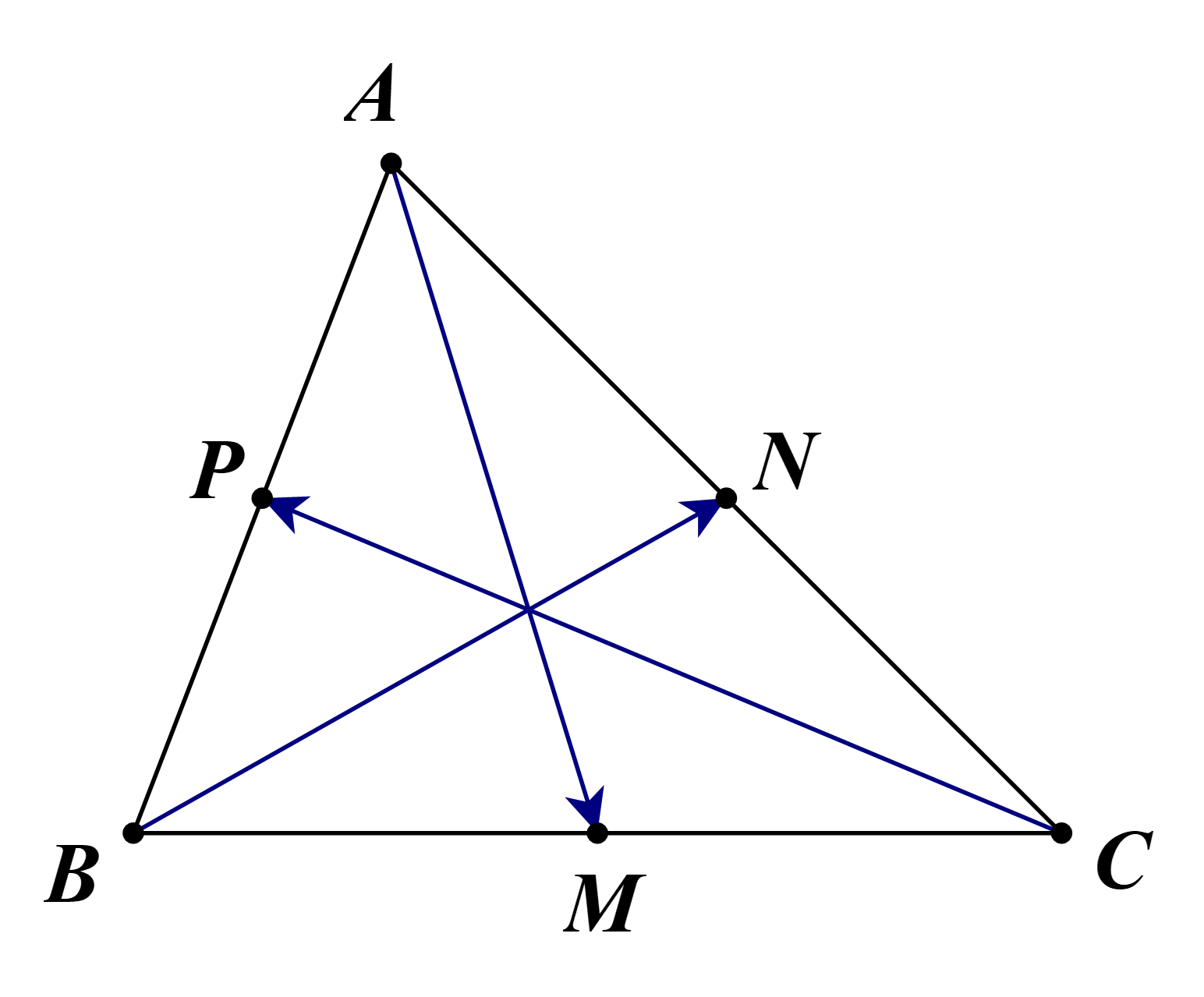
a) Ta có \(VT = \overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} \) (do M, N, P lần lượt là trung điểm của BC, CA, AB).
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BA} } \right) + \frac{1}{2}\left( {\overrightarrow {CB} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AC} } \right)\)
\( = \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 = \vec 0 = VP\).
Vậy ta có điều phải chứng minh.
b) Ta có \(VT = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\)
\( = \frac{1}{2}.2\overrightarrow {OP} + \frac{1}{2}.2\overrightarrow {ON} + \frac{1}{2}.2\overrightarrow {OM} \)
\( = \overrightarrow {OP} + \overrightarrow {ON} + \overrightarrow {OM} = VP\).
Vậy ta có điều phải chứng minh.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.