a) Tìm giá trị nhỏ nhất của A = 2x² – 8x + 1.

b) Tìm giá trị lớn nhất của B = –5x² – 4x + 1.

c) Tìm giá trị nhỏ nhất của biểu thức: \(A = \frac{2}{{6x - 5 - 9{x^2}}}\).

Lời giải

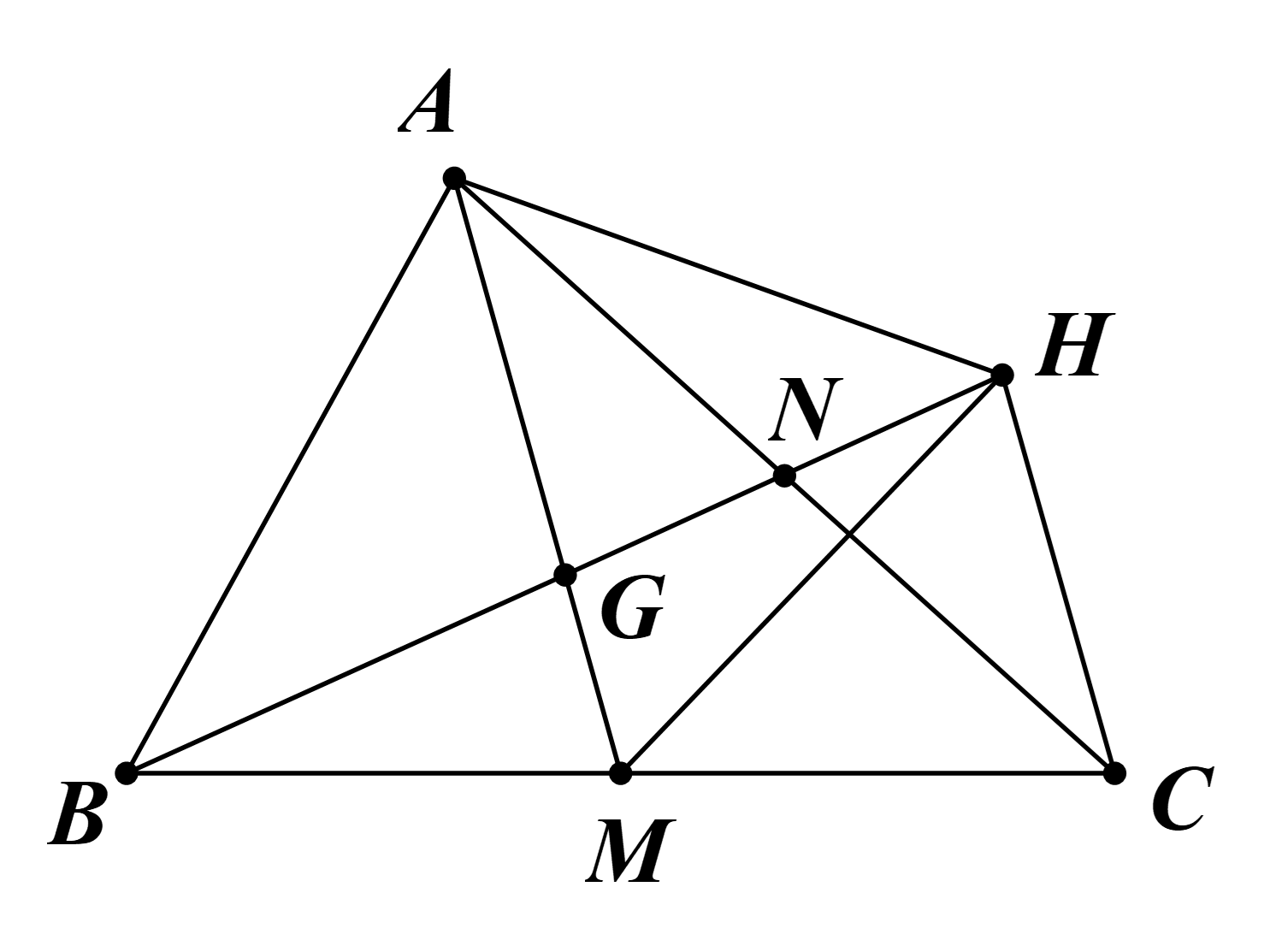
a) Gọi N là trung điểm AC.

Do H là điểm đối xứng của B qua G.

Suy ra G là trung điểm của BH.

Do đó \(GH = BG = \frac{2}{3}BN = 2GN\) (do G là trọng tâm tam giác ABC).

Vì vậy N là trung điểm GH (do 4 điểm B, G, N, H thẳng hàng).

Suy ra GN = NH.

Ta có \(\overrightarrow {AH} = \overrightarrow {AN} + \overrightarrow {NH} = \overrightarrow {AN} + \overrightarrow {GN} \)

\( = \overrightarrow {AN} + \frac{1}{3}\overrightarrow {BN} = \overrightarrow {AN} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)

\[ = \frac{4}{3}\overrightarrow {AN} - \frac{1}{3}\overrightarrow {AB} = \frac{4}{3}\left( {\frac{1}{2}\overrightarrow {AC} } \right) - \frac{1}{3}\overrightarrow {AB} \]

\[ = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \].

Ta có \(\overrightarrow {CH} = \overrightarrow {CN} + \overrightarrow {NH} = \overrightarrow {CN} + \overrightarrow {GN} \)

\( = \overrightarrow {CN} + \frac{1}{3}\overrightarrow {BN} = \overrightarrow {CN} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)

\[ = \overrightarrow {CN} - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AN} = - \frac{1}{2}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}.\frac{1}{2}\overrightarrow {AC} \]

\( = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \).

Vậy ta có điều phải chứng minh.

b) \(\overrightarrow {MH} = \overrightarrow {MB} + \overrightarrow {BH} = \frac{1}{2}\overrightarrow {CB} + \overrightarrow {BA} + \overrightarrow {AH} \)

\( = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AB} } \right) - \overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \)

\( = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).

Vậy ta có điều phải chứng minh.

Lời giải

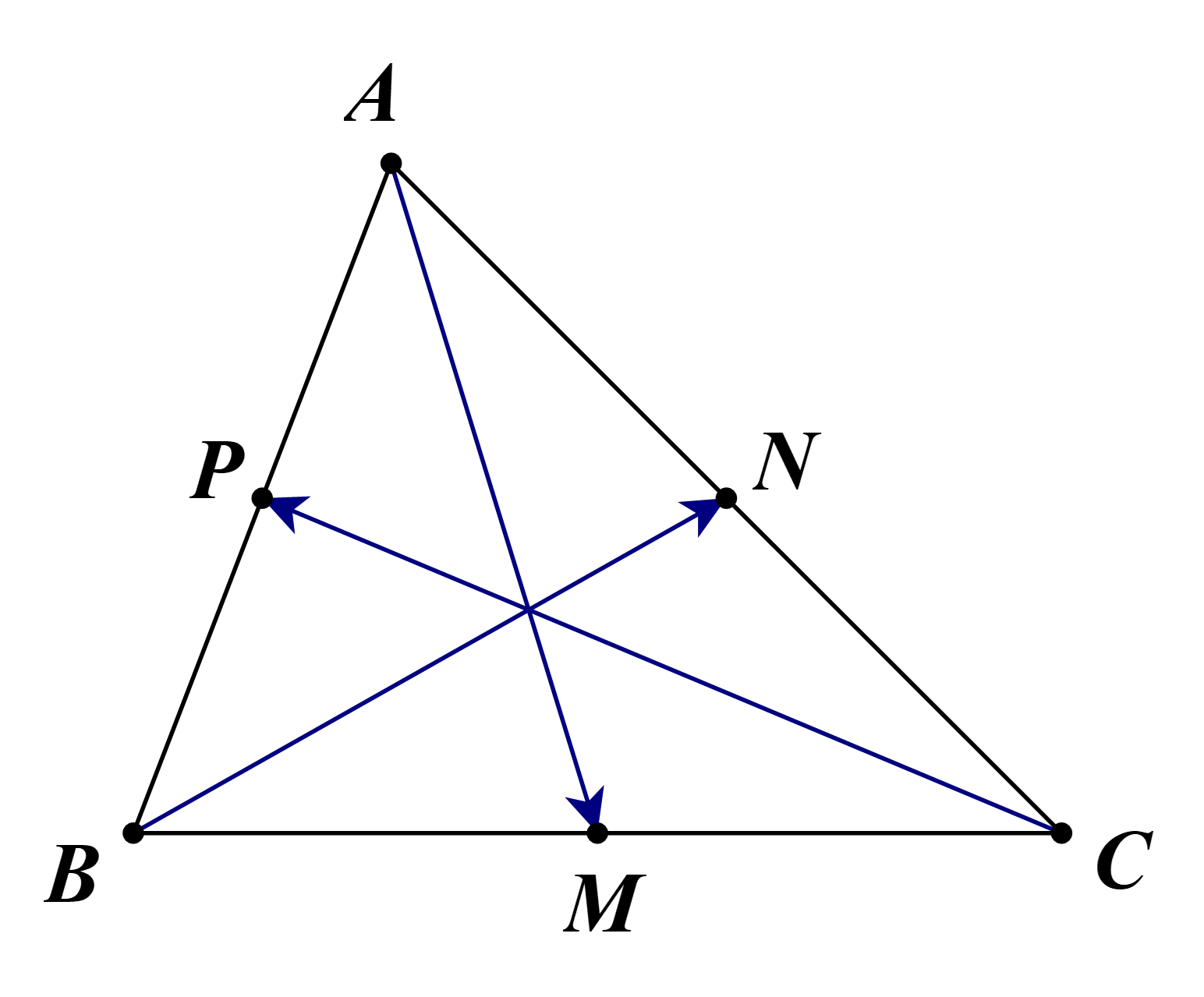
a) Ta có \(VT = \overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} \) (do M, N, P lần lượt là trung điểm của BC, CA, AB).

\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\)

\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BA} } \right) + \frac{1}{2}\left( {\overrightarrow {CB} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AC} } \right)\)

\( = \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 = \vec 0 = VP\).

Vậy ta có điều phải chứng minh.

b) Ta có \(VT = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\)

\( = \frac{1}{2}.2\overrightarrow {OP} + \frac{1}{2}.2\overrightarrow {ON} + \frac{1}{2}.2\overrightarrow {OM} \)

\( = \overrightarrow {OP} + \overrightarrow {ON} + \overrightarrow {OM} = VP\).

Vậy ta có điều phải chứng minh.