Câu hỏi:

13/07/2024 5,630

Cho hàm số y = (2m – 1)x + 2 (1) có đồ thị là đường thẳng d_m.

a) Vẽ đồ thị hàm số m = 1.

b) Tìm m để hàm số (1) đồng biến trên ℝ.

c) Tìm m để d_m đồng quy với d₁: y = x + 4 và d₂: y = –2x + 7.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

a) d_m: y = (2m – 1)x + 2 \(\left( {m \ne \frac{1}{2}} \right)\).

Với m = 1, ta có: y = x + 2.

Bảng giá trị của d_m khi m = 1:

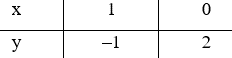
Media VietJack

Do đó đồ thị hàm số y = x + 2 là đường thẳng đi qua hai điểm (1; –1) và (0; 2).

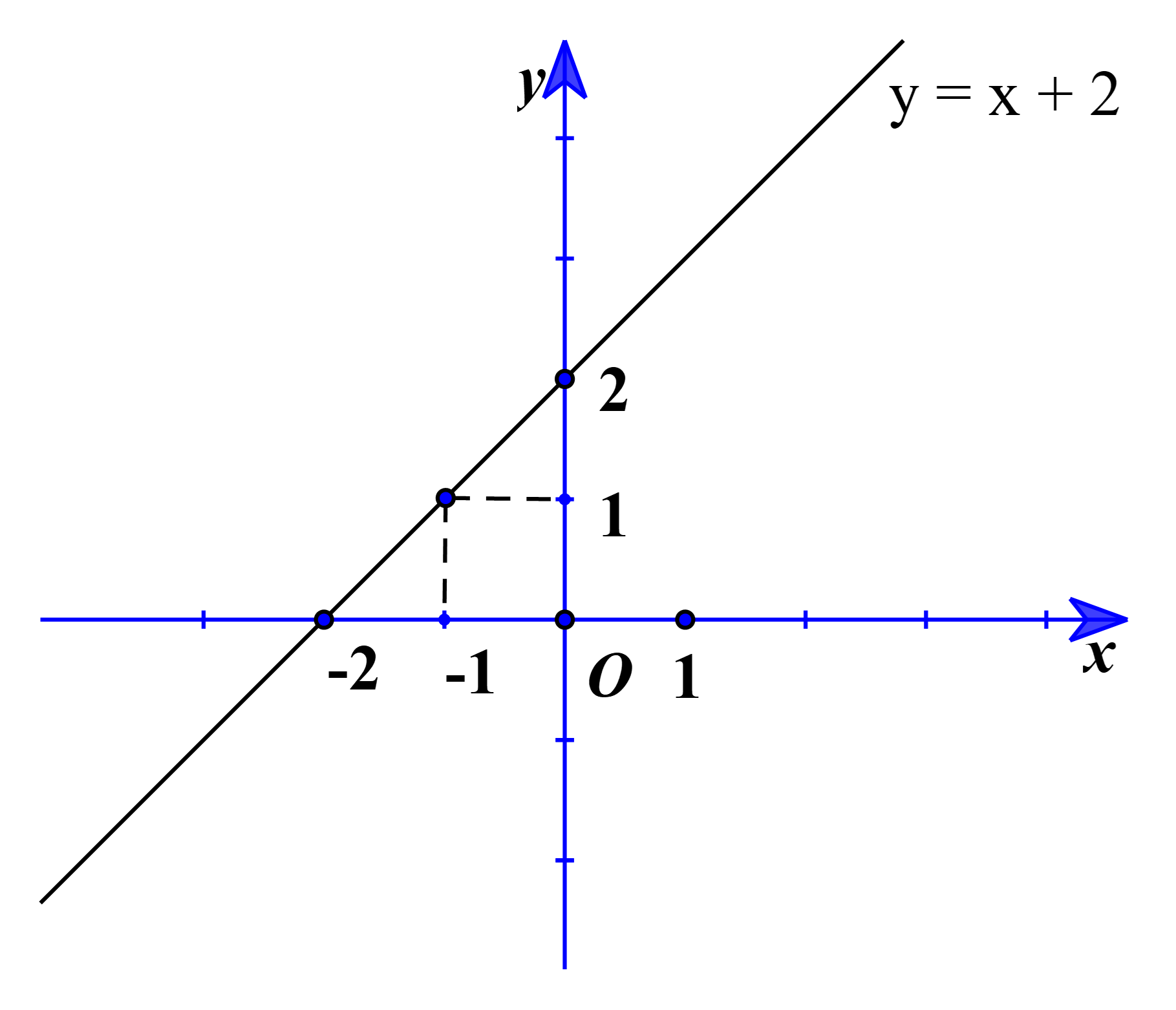
Media VietJack

b) Hàm số (1) đồng biến trên ℝ ⇔ 2m – 1 > 0.

\( \Leftrightarrow m > \frac{1}{2}\).

Vậy \(m > \frac{1}{2}\) thỏa mãn yêu cầu bài toán.

c) Phương trình hoành độ giao điểm của d₁ và d₂: x + 4 = –2x + 7

⇔ 3x = 3 ⇔ x = 1.

Với x = 1, ta có y = 1 + 4 = 5.

Do đó giao điểm của d₁ và d₂ là A(1; 5).

Để ba đường thẳng d, d₁ và d₂ đồng quy thì A(1; 5) ∈ d_m.

Û 5 = (2m – 1).1 + 2

Û 5 = 2m – 1 + 2

Û 2m = 4

Û m = 2 (nhận)

Vậy m = 2 thỏa mãn yêu cầu bài toán.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cách chuyển hỗn số thành số thập phân, ta làm như thế nào?

Xem đáp án

Lời giải

Muốn đổi hỗn số thành số thập phân, ta làm các bước sau:

Bước 1: Đưa hỗn số thành phân số:

– Lấy phần nguyên nhân với mẫu số, kết quả nhận được cộng thêm tử số;

– Thay kết quả ở trên thành tử số mới, giữ nguyên mẫu số, ta được một phân số từ hỗn số đã cho.

Bước 2: Đưa mẫu số về 10; 100; 1000; … và thực hiện đổi phân số thập phân về số thập phân.

Ví dụ: Đổi các hỗn số \(5\frac{1}{{10}}\) và \(5\frac{3}{4}\) thành số thập phân.

Hướng dẫn giải

Ta có: \(5\frac{1}{{10}} = \frac{{5 \times 10 + 1}}{{10}} = \frac{{51}}{{10}} = 5,1\);

\(5\frac{3}{4} = \frac{{5 \times 4 + 3}}{4} = \frac{{23}}{4} = \frac{{23 \times 25}}{{4 \times 25}} = \frac{{575}}{{100}} = 5,75\).

Câu 2

Cho hình vuông ABCD có cạnh bằng a. Gọi E là trung điểm cạnh BC, F là trung điểm cạnh AE. Tìm độ dài đoạn thẳng DF.

A. \(\frac{{a\sqrt {13} }}{4}\)

B. \(\frac{{a\sqrt 5 }}{4}\)

C. \(\frac{{a\sqrt 3 }}{2}\)

D. \(\frac{{3a}}{4}\)

Lời giải

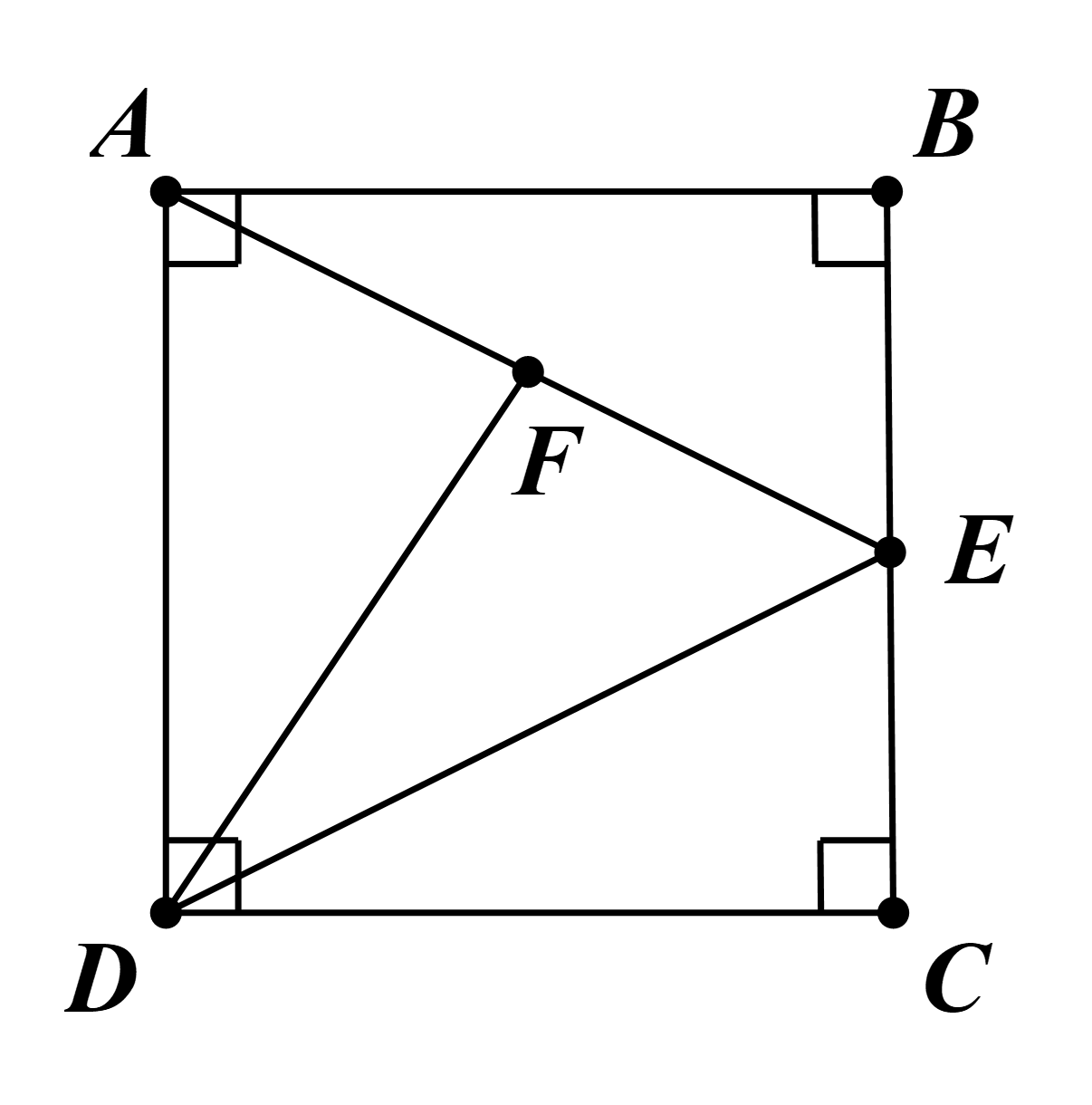
Media VietJack

Ta có E là trung điểm BC.

Suy ra \(CE = \frac{{BC}}{2} = \frac{a}{2}\).

Ta có AB = CD (do ABCD là hình vuông) và BE = CE (E là trung điểm BC).

Suy ra \(\sqrt {A{B^2} + B{E^2}} = \sqrt {C{D^2} + C{E^2}} \).

Do đó AE = DE.

Tam giác CDE vuông tại C: \(AE = DE = \sqrt {C{D^2} + C{E^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\).

Ta có \(D{F^2} = \frac{{2D{A^2} + 2D{E^2} - A{E^2}}}{4} = \frac{{2{a^2} + 2{{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2} - {{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2}}}{4} = \frac{{13{a^2}}}{{16}}\).

Vậy \(DF = \frac{{a\sqrt {13} }}{4}\).

Do đó ta chọn phương án A.

Câu 3