Câu hỏi:

13/07/2024 2,733

Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B₁, đựng cao Sao vàng, và đựng “Quy nhân sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau:

– Cách thứ nhất cắt được 3 hộp B₁, 1 hộp cao Sao vàng và 6 hộp Quy sâm.

– Cách thứ hai cắt được 2 hộp B₁, 3 hộp cao Sao vàng và 1 hộp Quy sâm.

Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B₁ tối thiểu là 900 hộp, số hộp cao Sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số bìa phải dùng là ít nhất?

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

Gọi x, y (x, y ≥ 0) lần lượt là số tấm bìa cắt theo cách thứ nhất, thứ hai.

Bài toán đưa đến tìm x, y ≥ 0 thỏa mãn hệ: \(\left\{ \begin{array}{l}3x + 2y \ge 900\\x + 3y \ge 1000\\6x + y = 900\end{array} \right.\) (1) sao cho L = x + y nhỏ nhất.

Vẽ d₁: 3x + 2y = 900, d₂: x + 3y = 1000, d₃: 6x + y = 900 trên cùng một hệ trục tọa độ Oxy.

Tiếp theo, ta lấy điểm A(0; 900). Khi đó ta có: \(\left\{ \begin{array}{l}3.0 + 2.900 = 1800 \ge 900\\0 + 3.900 = 2700 \ge 1000\\6.0 + 900 = 900\end{array} \right.\) (đúng).

Suy ra miền nghiệm của hệ (1) là một phần đường thẳng d₃ được tô màu như hình vẽ.

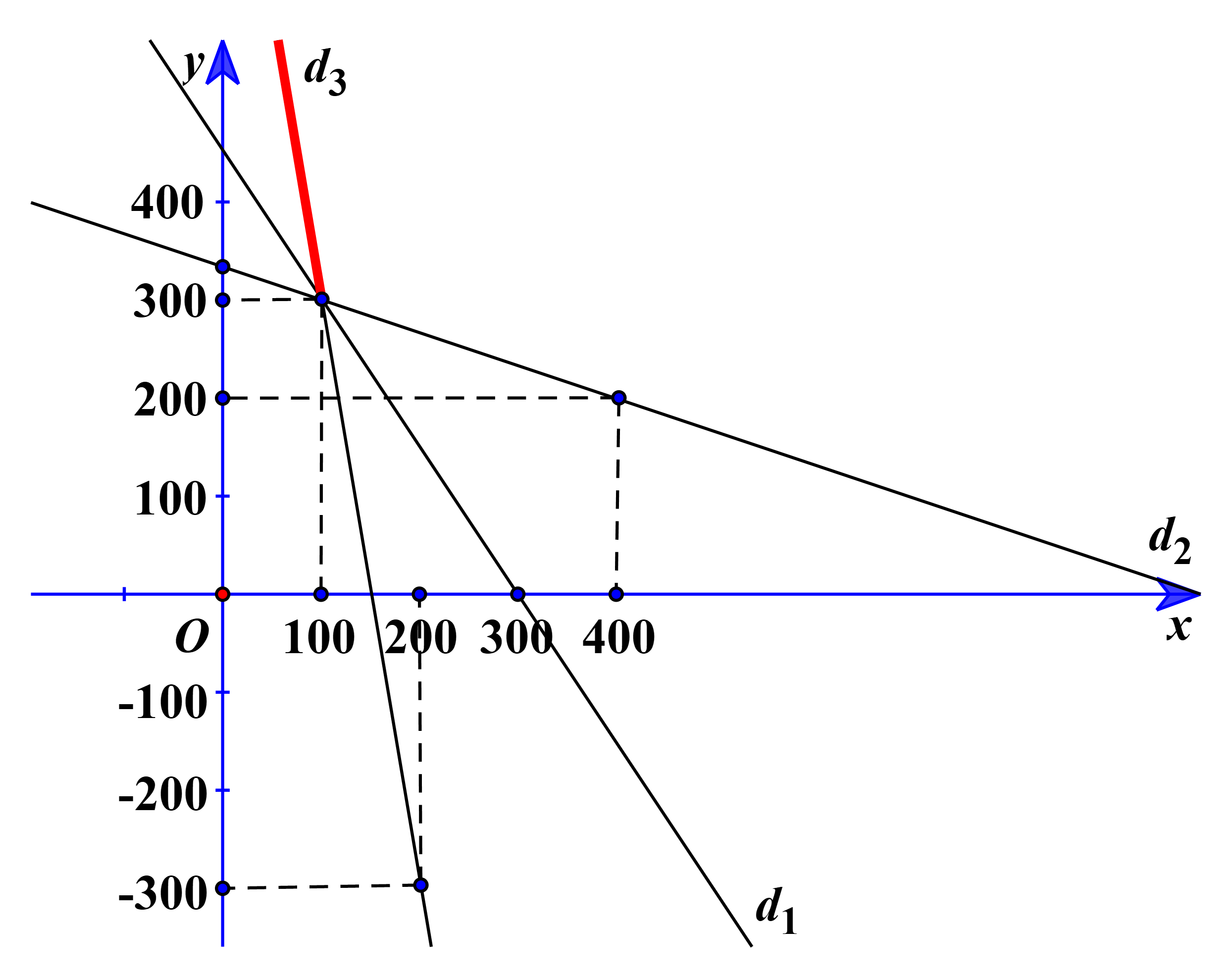
Media VietJack

Ta có giao điểm của d₃ và Oy là A(0; 900) và giao điểm của d₃ và d₂ là B(100; 300).

Từ miền nghiệm, ta thấy L nhỏ nhất khi (x; y) là một trong hai điểm A(0; 900) và B(100; 300).

L(0; 900) = 0 + 900 = 900.

L(100; 300) = 100 + 300 = 400.

Do đó L nhỏ nhất khi x = 100, y = 300.

Vậy người ta cần cắt 100 tấm bìa theo cách thứ nhất, 300 tấm bìa theo cách thứ hai thì tổng số bìa phải dùng là ít nhất.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cách chuyển hỗn số thành số thập phân, ta làm như thế nào?

Xem đáp án

Lời giải

Muốn đổi hỗn số thành số thập phân, ta làm các bước sau:

Bước 1: Đưa hỗn số thành phân số:

– Lấy phần nguyên nhân với mẫu số, kết quả nhận được cộng thêm tử số;

– Thay kết quả ở trên thành tử số mới, giữ nguyên mẫu số, ta được một phân số từ hỗn số đã cho.

Bước 2: Đưa mẫu số về 10; 100; 1000; … và thực hiện đổi phân số thập phân về số thập phân.

Ví dụ: Đổi các hỗn số \(5\frac{1}{{10}}\) và \(5\frac{3}{4}\) thành số thập phân.

Hướng dẫn giải

Ta có: \(5\frac{1}{{10}} = \frac{{5 \times 10 + 1}}{{10}} = \frac{{51}}{{10}} = 5,1\);

\(5\frac{3}{4} = \frac{{5 \times 4 + 3}}{4} = \frac{{23}}{4} = \frac{{23 \times 25}}{{4 \times 25}} = \frac{{575}}{{100}} = 5,75\).

Câu 2

Cho hình vuông ABCD có cạnh bằng a. Gọi E là trung điểm cạnh BC, F là trung điểm cạnh AE. Tìm độ dài đoạn thẳng DF.

A. \(\frac{{a\sqrt {13} }}{4}\)

B. \(\frac{{a\sqrt 5 }}{4}\)

C. \(\frac{{a\sqrt 3 }}{2}\)

D. \(\frac{{3a}}{4}\)

Lời giải

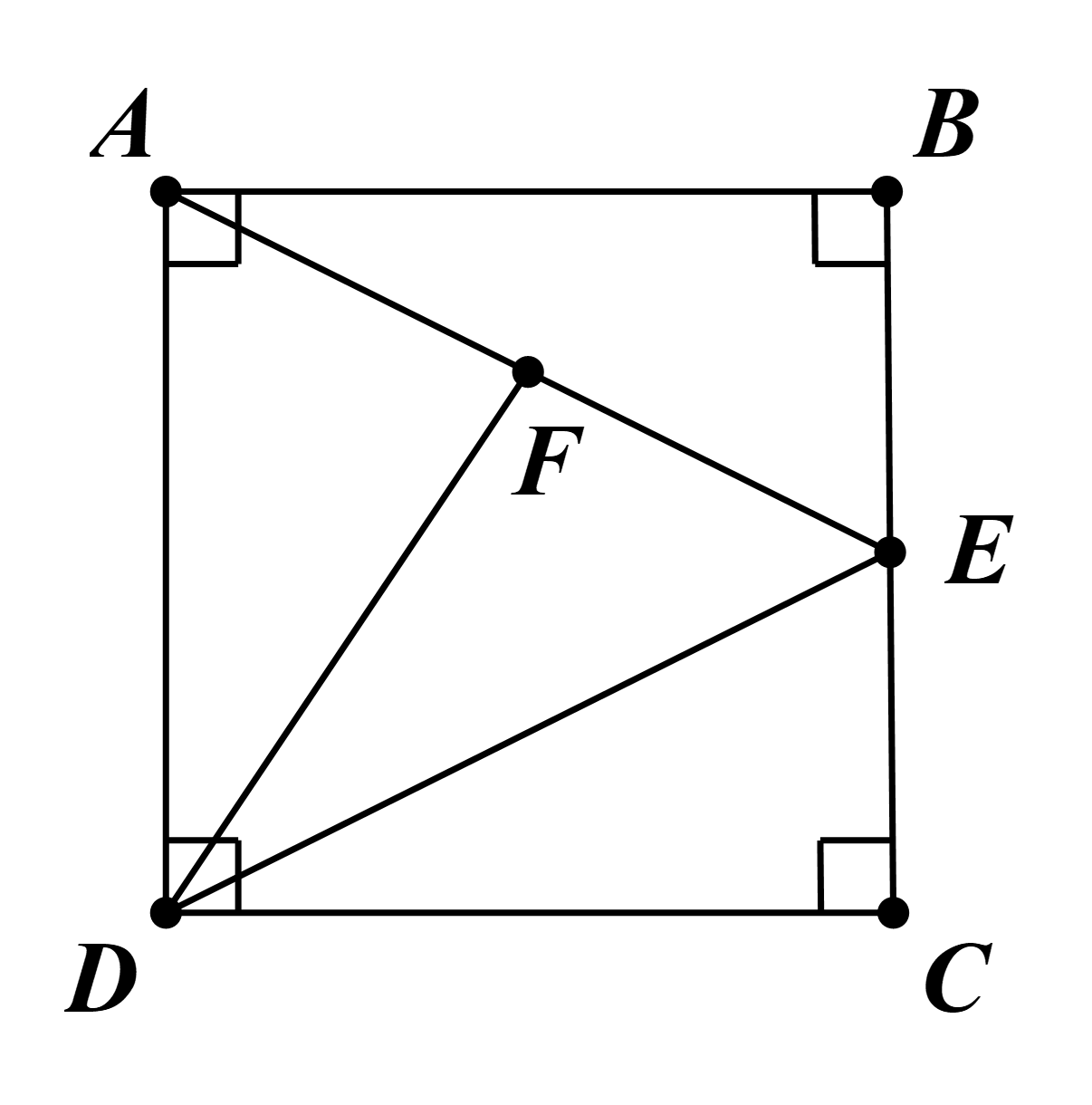
Media VietJack

Ta có E là trung điểm BC.

Suy ra \(CE = \frac{{BC}}{2} = \frac{a}{2}\).

Ta có AB = CD (do ABCD là hình vuông) và BE = CE (E là trung điểm BC).

Suy ra \(\sqrt {A{B^2} + B{E^2}} = \sqrt {C{D^2} + C{E^2}} \).

Do đó AE = DE.

Tam giác CDE vuông tại C: \(AE = DE = \sqrt {C{D^2} + C{E^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\).

Ta có \(D{F^2} = \frac{{2D{A^2} + 2D{E^2} - A{E^2}}}{4} = \frac{{2{a^2} + 2{{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2} - {{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2}}}{4} = \frac{{13{a^2}}}{{16}}\).

Vậy \(DF = \frac{{a\sqrt {13} }}{4}\).

Do đó ta chọn phương án A.

Câu 3