Cho (O; R), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.

a) Chứng minh: Tam giác OBA vuông tại B và Tam giác OAK cân tại K.

b) Đường thẳng KI cắt AB tại M. Chứng minh rằng KM là tiếp tuyến của đường tròn (O).
c) Tính chu vi tam giác AMK theo R.

Lời giải

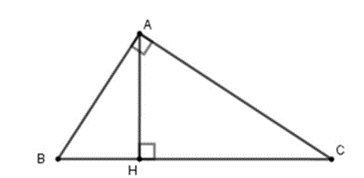
a) Xét ∆ABH và ∆CBA có:

\(\widehat {BHA} = \widehat {BAC} = 90^\circ \)

\(\widehat {ABC}\) chung.

Do đó  (g.g)

Suy ra \(\frac{{AB}}{{CB}} = \frac{{BH}}{{BA}}\) (tỉ số đồng dạng)

Do đó AB² = BH . BC.

b) Vì tam giác AHC vuông tại H nên  \(\widehat {HCA} + \widehat {HAC} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Mà \(\widehat {BAH} + \widehat {HAC} = \widehat {BAC} = 90^\circ \)

Suy ra \(\widehat {BAH} = \widehat {HCA}\)

Xét ∆AHB và ∆CHA có:

\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)

\(\widehat {BAH} = \widehat {HCA}\)(chứng minh trên)

Do đó  (g.g)

Suy ra \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\) (tỉ số đồng dạng)

Do đó AH² = BH . CH.

c) Ta có \[{S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\]

Suy ra AB . AC = AH . BC.

d) Xét ∆CAH và ∆CBA có:

\(\widehat {CHA} = \widehat {BAC} = 90^\circ \).

\(\widehat {ACB}\) chung.

Do đó  (g.g)

Suy ra \(\frac{{AC}}{{BC}} = \frac{{HC}}{{AC}}\) (tỉ số đồng dạng)

Do đó AC² = CH . BC.

Lời giải

a) Ta có:

\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} \)

= \(\overrightarrow {EA} + \overrightarrow {AB} + \overrightarrow {CD} \)

= \(\overrightarrow {EB} + \overrightarrow {CD} \)

= \(\overrightarrow {ED} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} \)

= \(\overrightarrow {ED} + \overrightarrow {CB} + (\overrightarrow {BD} + \overrightarrow {DB} )\)

= \(\overrightarrow {CB} + \overrightarrow {ED} \)

Vậy \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} \) = \(\overrightarrow {CB} + \overrightarrow {ED} \)

b) Ta có:

\(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} \)

= \(\overrightarrow {AC} + \overrightarrow {CD} + \overrightarrow {CE} \)

= \(\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {CD} \)

= \(\overrightarrow {AE} + \overrightarrow {CD} \)

= \(\overrightarrow {AE} + \overrightarrow {CB} + \overrightarrow {BD} \)

= \(\overrightarrow {A{\rm{E}}} - \overrightarrow {BD} + \overrightarrow {CB} \)

Vậy \(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} \) = \(\overrightarrow {A{\rm{E}}} - \overrightarrow {BD} + \overrightarrow {CB} \).