Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN).
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
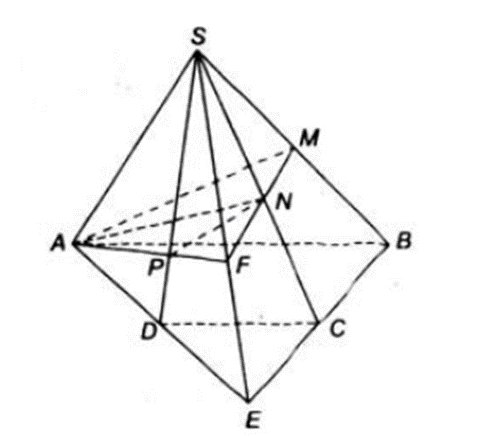
a) Gọi E là giao điểm của AD và BC.
Ta có \[\left\{ \begin{array}{l}E \in AD \Rightarrow E \in \left( {SAD} \right)\\E \in BC \Rightarrow E \in \left( {SBC} \right)\end{array} \right.\]
Do đó E = (SAD) ∩ (SBC)
Mà S = (SAD) ∩ (SBC)
Suy ra SE = (SAD) ∩ (SBC).
b) Trong mp(SBE) gọi giao điểm của MN và SE là F.

Trong mp(SAD) gọi giao điểm của AF là SD là P.
Suy ra P = SD ∩ (AMN).
c) Ta có

Vậy thiết diện thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN) là tứ giác AMNP.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
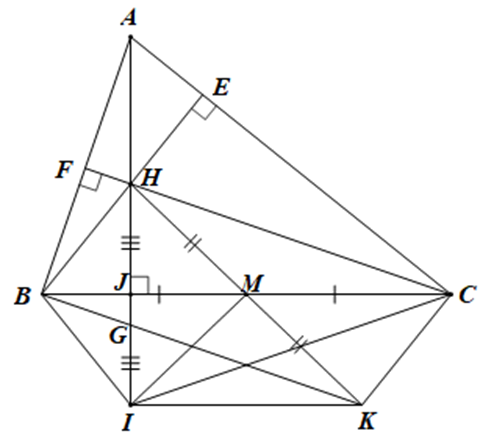
a) Xét tứ giác BHCK có:
MH = MK và MB = MI
Suy ra: BHCK là hình bình hành.
b) Vì BHCK là hình bình hành (chứng minh câu a)
Suy ra: BK // HC và CK // BH (tính chất hình bình hành)
Mà CH ⊥ AB và BH ⊥ AC
Suy ra: BK ⊥ AB và CK ⊥ AC.
c) Vì I đối xứng với H qua BC nên BC là đường trung trực của HI
Mà M thuộc BC, suy ra MH = MI (tính chất đường trung trực)
Mà \[MH = MK = \frac{1}{2}HK\]
Suy ra: \[MI = MH = MK = \frac{1}{2}HK\]
Do đó tam giác HIK vuông tại I hay HI ⊥ IK
Mà BC ⊥ HI (do BC là đường trung trực của HI)
Suy ra IK // BC
Do đó BIKC là hình thang (1)
Ta có BC là đường trung trực của HI, suy ra CI = CH
Mà CH = BK (vì BKCH là hình bình hành)
Suy ra BK = CI (2)
Từ (1) và (2) suy ra BICK là hình thang cân (dấu hiệu nhận biết)
d) Gọi giao điểm của BC và HI là J.
Vì BK // CH nên GHCK là hình thang
Để hình thang GHCK là hình thang cân thì \(\widehat {GHC} = \widehat {KCH}\)
Mà \(\widehat {HCK} + \widehat {HCA} = 90^\circ \) và \(\widehat {GHC} + \widehat {HCB} = 90^\circ \) (vì tam giác HJC vuông tại J)
Suy ra \(\widehat {HCA} = \widehat {HCB}\)
Do đó CH là đường phân giác của tam giác ABC
Lại có CH là đường cao của tam giác ABC
Suy ra tam giác ABC cân tại C
Vậy tam giác ABC cân tại C thì GHCK là hình thang cân.
Lời giải
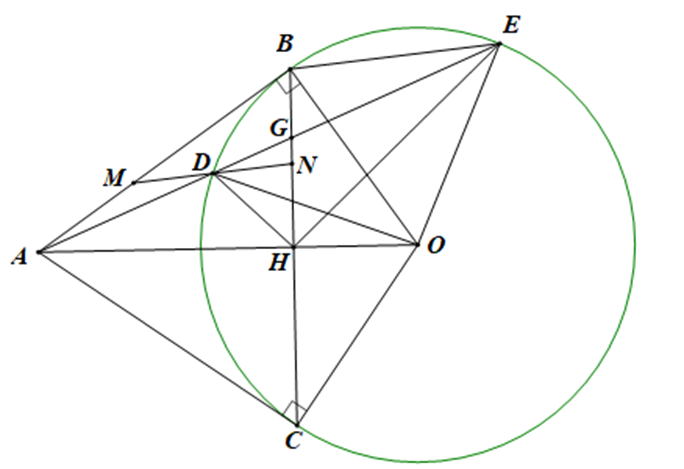
a) Vì AB, AC là tiếp tuyến của (O) nên AB ⊥ OB, AC ⊥ OC
Do đó \(\widehat {ABO} = \widehat {ACO} = 90^\circ \)
Suy ra A, B, O, C cùng thuộc đường tròn đường kính AO.
b) Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A, suy ra AB = AC
Hay A thuộc trung trực của BC
Mà O thuộc trung trực của BC (vì OB = OC)
Suy ra AO là trung trực của BC
Do đó AO ⊥ BC.
Xét tam giác ABO vuông tại B có BH ⊥ AO
Suy ra OB2 = OH . OA (hệ thức lượng trong tam giác vuông)
Mà OB = OD (cùng là bán kính của (O)).
Suy ra OD2 = OH . OA.
Do đó \(\frac{{OD}}{{OA}} = \frac{{OH}}{{O{\rm{D}}}}\)
Xét tam giác OHD và tam giác ODA có
\(\frac{{OD}}{{OA}} = \frac{{OH}}{{O{\rm{D}}}}\) (Chứng minh trên)
\(\widehat {DOA}\) là góc chung
Suy ra (c.g.c)
c) Ta có OB2 = OH . OA (chứng minh câu b)
Mà OB = OE, suy ra OE2 = OH . OA
Do đó \(\frac{{OH}}{{OE}} = \frac{{OE}}{{OA}}\)
Xét tam giác OHE và tam giác OEA có
\(\frac{{OH}}{{OE}} = \frac{{OE}}{{OA}}\) (Chứng minh trên)
\(\widehat {EOA}\) là góc chung
Suy ra (c.g.c)
Do đó \(\widehat {EHO} = \widehat {A{\rm{E}}O}\) (hai góc tương ứng)
Mặt khác \(\widehat {DEO} = \widehat {EDO}\) (vì tam giác ODE cân tại O)
Suy ra \(\widehat {EHO} = \widehat {{\rm{ED}}O}\)
Xét tứ giác HDEO có \(\widehat {EHO} = \widehat {{\rm{ED}}O}\), mà hai góc này cùng nhìn cạnh EO trong tứ giác
Suy ra tứ giác HDEO nội tiếp
Do đó \(\widehat {DHA} = \widehat {AEO} = \widehat {OHE}\)
Suy ra \(\widehat {DHB} = \widehat {BHE}\) nên \(HB\) là tia phân giác của góc DHE.
Hay CB trùng với tia phân giác của góc DHE.
d) Gọi G là giao điểm của BC và AE
Do HG là tia phân giác của \(\widehat {DHE}\)nên \(\frac{{{\rm{GD}}}}{{{\rm{GE}}}} = \frac{{HD}}{{HE}}\) (1)
Mà HA ⊥ HG
Suy ra HA là tia phân giác ngoài của tam giác HED
Do đó \(\frac{{A{\rm{D}}}}{{A{\rm{E}}}} = \frac{{H{\rm{D}}}}{{HE}}\) (2)
Từ (1) và (2) suy ra \(\frac{{{\rm{GD}}}}{{{\rm{GE}}}} = \frac{{A{\rm{D}}}}{{A{\rm{E}}}}\left( { = \frac{{H{\rm{D}}}}{{HE}}} \right)\) (3)
Xét DABE có DM // BE nên \(\frac{{M{\rm{D}}}}{{BE}} = \frac{{A{\rm{D}}}}{{A{\rm{E}}}}\) (hệ quả định lí Thales) (4)
Xét DGBE có DN // BE nên \(\frac{{{\rm{ND}}}}{{BE}} = \frac{{{\rm{GD}}}}{{{\rm{GE}}}}\) (hệ quả định lí Thales) (5)
Từ (3), (4) và (5), suy ra \(\frac{{{\rm{MD}}}}{{BE}} = \frac{{{\rm{ND}}}}{{{\rm{BE}}}}\)
Hay MD = ND
Do đó D là trung điểm của MN
Vậy D là trung điểm của MN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.