Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Ta thấy
Hiệu giữa 3 và 17 là 14
Hiệu giữa 17 và 59 là 42 = 14 . 3
Hiệu giữa 59 và 185 là 126 = 42 . 3
Hiệu giữa 185 và 563 là 378 = 126 . 3
Suy ra quy luật hiệu của hai số sau sẽ gấp 3 lần hiệu của hai số trước (có lặp lại số ở giữa 2 số kia)
Vậy số cần điền là : 378 . 3 + 563 = 1697.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
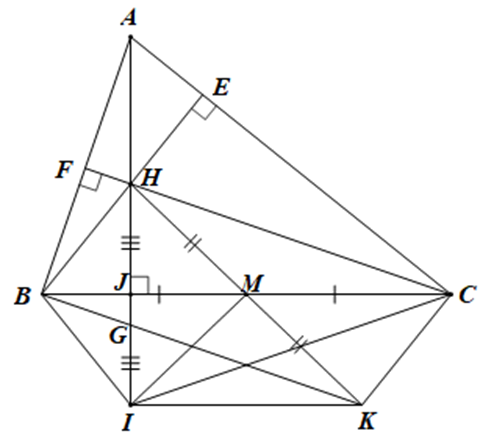
a) Xét tứ giác BHCK có:
MH = MK và MB = MI
Suy ra: BHCK là hình bình hành.
b) Vì BHCK là hình bình hành (chứng minh câu a)
Suy ra: BK // HC và CK // BH (tính chất hình bình hành)
Mà CH ⊥ AB và BH ⊥ AC
Suy ra: BK ⊥ AB và CK ⊥ AC.
c) Vì I đối xứng với H qua BC nên BC là đường trung trực của HI
Mà M thuộc BC, suy ra MH = MI (tính chất đường trung trực)
Mà \[MH = MK = \frac{1}{2}HK\]
Suy ra: \[MI = MH = MK = \frac{1}{2}HK\]
Do đó tam giác HIK vuông tại I hay HI ⊥ IK
Mà BC ⊥ HI (do BC là đường trung trực của HI)
Suy ra IK // BC
Do đó BIKC là hình thang (1)
Ta có BC là đường trung trực của HI, suy ra CI = CH
Mà CH = BK (vì BKCH là hình bình hành)
Suy ra BK = CI (2)
Từ (1) và (2) suy ra BICK là hình thang cân (dấu hiệu nhận biết)
d) Gọi giao điểm của BC và HI là J.
Vì BK // CH nên GHCK là hình thang
Để hình thang GHCK là hình thang cân thì \(\widehat {GHC} = \widehat {KCH}\)
Mà \(\widehat {HCK} + \widehat {HCA} = 90^\circ \) và \(\widehat {GHC} + \widehat {HCB} = 90^\circ \) (vì tam giác HJC vuông tại J)
Suy ra \(\widehat {HCA} = \widehat {HCB}\)
Do đó CH là đường phân giác của tam giác ABC
Lại có CH là đường cao của tam giác ABC
Suy ra tam giác ABC cân tại C
Vậy tam giác ABC cân tại C thì GHCK là hình thang cân.
Lời giải
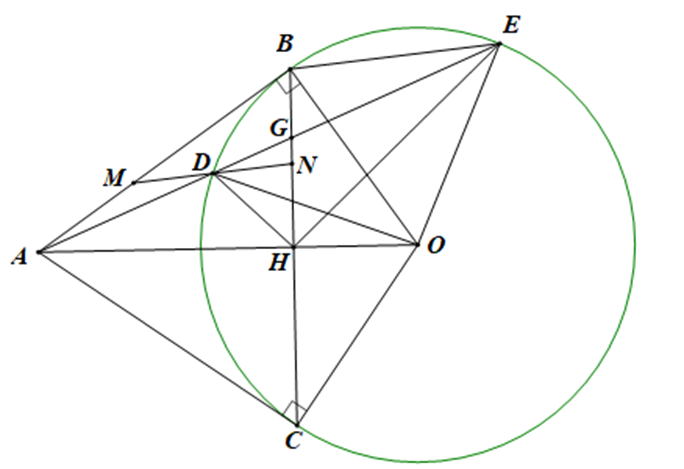
a) Vì AB, AC là tiếp tuyến của (O) nên AB ⊥ OB, AC ⊥ OC
Do đó \(\widehat {ABO} = \widehat {ACO} = 90^\circ \)
Suy ra A, B, O, C cùng thuộc đường tròn đường kính AO.
b) Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A, suy ra AB = AC
Hay A thuộc trung trực của BC
Mà O thuộc trung trực của BC (vì OB = OC)
Suy ra AO là trung trực của BC
Do đó AO ⊥ BC.
Xét tam giác ABO vuông tại B có BH ⊥ AO
Suy ra OB2 = OH . OA (hệ thức lượng trong tam giác vuông)
Mà OB = OD (cùng là bán kính của (O)).
Suy ra OD2 = OH . OA.
Do đó \(\frac{{OD}}{{OA}} = \frac{{OH}}{{O{\rm{D}}}}\)
Xét tam giác OHD và tam giác ODA có
\(\frac{{OD}}{{OA}} = \frac{{OH}}{{O{\rm{D}}}}\) (Chứng minh trên)
\(\widehat {DOA}\) là góc chung
Suy ra (c.g.c)
c) Ta có OB2 = OH . OA (chứng minh câu b)
Mà OB = OE, suy ra OE2 = OH . OA
Do đó \(\frac{{OH}}{{OE}} = \frac{{OE}}{{OA}}\)
Xét tam giác OHE và tam giác OEA có
\(\frac{{OH}}{{OE}} = \frac{{OE}}{{OA}}\) (Chứng minh trên)
\(\widehat {EOA}\) là góc chung
Suy ra (c.g.c)
Do đó \(\widehat {EHO} = \widehat {A{\rm{E}}O}\) (hai góc tương ứng)
Mặt khác \(\widehat {DEO} = \widehat {EDO}\) (vì tam giác ODE cân tại O)
Suy ra \(\widehat {EHO} = \widehat {{\rm{ED}}O}\)
Xét tứ giác HDEO có \(\widehat {EHO} = \widehat {{\rm{ED}}O}\), mà hai góc này cùng nhìn cạnh EO trong tứ giác
Suy ra tứ giác HDEO nội tiếp
Do đó \(\widehat {DHA} = \widehat {AEO} = \widehat {OHE}\)
Suy ra \(\widehat {DHB} = \widehat {BHE}\) nên \(HB\) là tia phân giác của góc DHE.
Hay CB trùng với tia phân giác của góc DHE.
d) Gọi G là giao điểm của BC và AE
Do HG là tia phân giác của \(\widehat {DHE}\)nên \(\frac{{{\rm{GD}}}}{{{\rm{GE}}}} = \frac{{HD}}{{HE}}\) (1)
Mà HA ⊥ HG
Suy ra HA là tia phân giác ngoài của tam giác HED
Do đó \(\frac{{A{\rm{D}}}}{{A{\rm{E}}}} = \frac{{H{\rm{D}}}}{{HE}}\) (2)
Từ (1) và (2) suy ra \(\frac{{{\rm{GD}}}}{{{\rm{GE}}}} = \frac{{A{\rm{D}}}}{{A{\rm{E}}}}\left( { = \frac{{H{\rm{D}}}}{{HE}}} \right)\) (3)
Xét DABE có DM // BE nên \(\frac{{M{\rm{D}}}}{{BE}} = \frac{{A{\rm{D}}}}{{A{\rm{E}}}}\) (hệ quả định lí Thales) (4)
Xét DGBE có DN // BE nên \(\frac{{{\rm{ND}}}}{{BE}} = \frac{{{\rm{GD}}}}{{{\rm{GE}}}}\) (hệ quả định lí Thales) (5)
Từ (3), (4) và (5), suy ra \(\frac{{{\rm{MD}}}}{{BE}} = \frac{{{\rm{ND}}}}{{{\rm{BE}}}}\)
Hay MD = ND
Do đó D là trung điểm của MN
Vậy D là trung điểm của MN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.