Tính chiều cao CH của tháp ở bên kia sông biết AB = 25 m, \(\widehat {HAC} = 32^\circ \), \(\widehat {HBC} = 43^\circ \), và ba điểm A, B, H thẳng hàng. (kết quả làm tròn đến chữ số thập phân thứ nhất).
Tính chiều cao CH của tháp ở bên kia sông biết AB = 25 m, \(\widehat {HAC} = 32^\circ \), \(\widehat {HBC} = 43^\circ \), và ba điểm A, B, H thẳng hàng. (kết quả làm tròn đến chữ số thập phân thứ nhất).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét tam giác CAH vuông tại H có:
\(\tan \widehat {HAC} = \tan 32^\circ = \frac{{CH}}{{HA}} \Rightarrow HA = \frac{{CH}}{{\tan 32^\circ }}\)
Xét tam giác CBH vuông tại H có:
\(\tan \widehat {HBC} = \tan 43^\circ = \frac{{CH}}{{BH}} \Rightarrow BH = \frac{{CH}}{{\tan 43^\circ }}\)
Ta có:
\(\begin{array}{l}AB = AH - BH\\ \Rightarrow CH\left( {\frac{1}{{\tan 32^\circ }} - \frac{1}{{\tan 43^\circ }}} \right) = 25 \Rightarrow CH = \frac{{25}}{{\left( {\frac{1}{{\tan 32^\circ }} - \frac{1}{{\tan 43^\circ }}} \right)}} \approx 47,4\,\,(m)\end{array}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
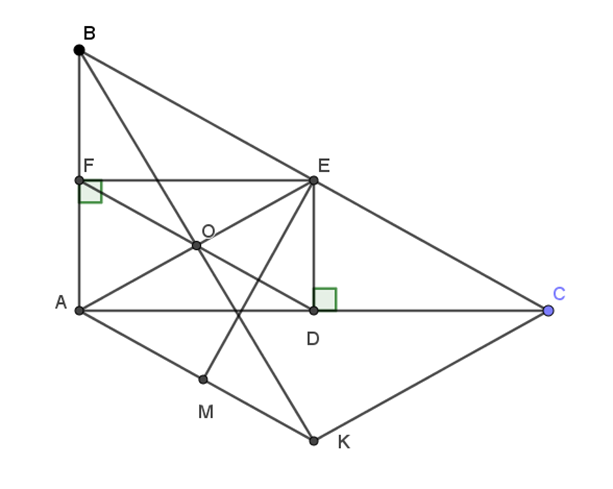
a)
EF vuông góc với AB do đó \(\widehat {AFE} = 90^\circ \)
ED vuông góc với AC do đó \(\widehat {ADE} = 90^\circ \)
Tứ giác ADEF có:
\(\widehat {FAD} = 90^\circ \)
\(\widehat {AFE} = 90^\circ \)
\(\widehat {ADE} = 90^\circ \)
Do đó, ADEF là hình chữ nhật
b)
K đối xứng với E qua D
Do đó D là trung điểm của EK
ED vuông góc với AC, AB vuông góc với AC
Do đó, ED song song với AB
Tam giác ABC có:
E là trung điểm của BC
ED song song với AB
Do đó, D là trung điểm của AC
Tứ giác AECK có:
D là trung điểm của AC, EK
Do đó, AECK là hình bình hành mà EK vuông góc với AC
Do đó, AECK là hình thoi
c)
ADEF là hình chữ nhật, DF và AE giao nhau tại O
Nên O là trung điểm của DF, AE và DF = AE
AECK là hình thoi nên AK = EC, AK song song với EC
AK = EC, BE = EC nên AK = BE
Tứ giác ABEK có:
AK = BE
AK song song với BE
Do đó, ABEK là hình bình hành
Do đó, AE, BK cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm của AE, O là trung điểm của BK
Do đó, B, O, K thẳng hàng
d)
Tam giác AME vuông tại M có MO là đường trung tuyến
\(MO = \frac{1}{2}AE = \frac{1}{2}DF\)
Tam giác FMD có:
\(MO = \frac{1}{2}DF\)
MO là đường trung tuyến
Do đó, FMD vuông tại M
\( \Rightarrow \widehat {DMF} = 90^\circ \)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
\(\sin A = \cos B + \cos C = 2cos\frac{{B + C}}{2}.cos\frac{{B - C}}{2}\)
\( = 2\sin \frac{A}{2}.cos\frac{{B - C}}{2}\)
\( \Leftrightarrow 2\sin \frac{A}{2}.cos\frac{A}{2} = 2\sin \frac{A}{2}.cos\frac{{B - C}}{2}\)
\( \Leftrightarrow cos\frac{A}{2} = cos\frac{{B - C}}{2} \Rightarrow \frac{A}{2} = \frac{{B - C}}{2}\)
\(\begin{array}{l} \Rightarrow \widehat B = \widehat A + \widehat C\\ \Rightarrow 2\widehat B = 180^\circ \Rightarrow \widehat B = 90^\circ \end{array}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập