Câu hỏi:
11/07/2024 8,757
Cho tam giác nhọn ABC, vẽ các đường cao BD, CE.
a) Chứng minh rằng: ∆ADB đồng dạng với ∆AEC.
b) Chúng minh rằng: ∆ADE đồng dạng với ∆ABC.
c) Vẽ EF vuông góc với AC tại F. Chứng minh rằng: AE.DF = AF.BE.
d) Gọi M, N lần lượt là trung điểm của các doạn thắng BD, CE. Chứng minh rằng: Hai góc BAC và MAN có chung tia phân giác.
Cho tam giác nhọn ABC, vẽ các đường cao BD, CE.
a) Chứng minh rằng: ∆ADB đồng dạng với ∆AEC.
b) Chúng minh rằng: ∆ADE đồng dạng với ∆ABC.
c) Vẽ EF vuông góc với AC tại F. Chứng minh rằng: AE.DF = AF.BE.
d) Gọi M, N lần lượt là trung điểm của các doạn thắng BD, CE. Chứng minh rằng: Hai góc BAC và MAN có chung tia phân giác.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
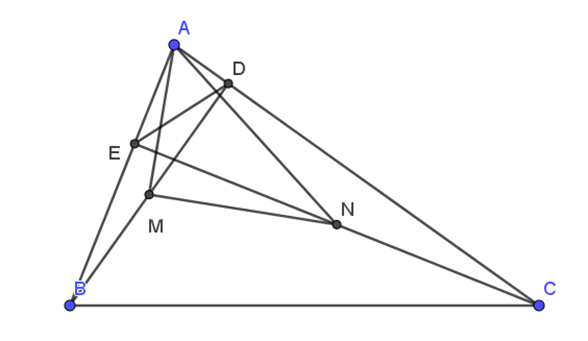
a) Xét tam giác ADB và tam giác AEC có:
\(\widehat A\) chung
\(\widehat {ADB} = \widehat {AEC} = 90^\circ \) (gt)
Do đó, tam giác ADB đồng dạng với tam giác AEC (g.g)
b) Vì tam giác ADB đồng dạng với tam giác AEC (câu a) nên ta có:
\(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\)
Xét tam giác ADE và tam giác ABC có:
\(\widehat A\) chung
\(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\) (cmt)
Do đó, tam giác ADE đồng dạng với tam giác ABC (c.g.c)
c) Ta có:
EF vuông góc với AC
BD vuông góc với AC
Do đó, EF song song với BD
Xét tam giác ADB có:
EF song song với BD
Do đó, \(\frac{{AE}}{{EB}} = \frac{{AF}}{{FD}}\) (định lý Talet)
Hay: AE. FD = AF.BE
d)
M là trung điểm BD nên BD = 2MB
N là trung điểm CE nên CE = 2NC
Vì tam giác ADB đồng dạng với tam giác AEC (câu a)
Do đó, \(\frac{{AB}}{{AC}} = \frac{{DB}}{{EC}} = \frac{{MB}}{{NC}}\).
Gọi H là giao điểm của hai đường cao BD và CE.
Xét tam giác HEB và tam giác HDC có:
\(\widehat {HEB} = \widehat {HDC} = 90^\circ \)
\(\widehat {EHB} = \widehat {DHC}\) (đối đỉnh)
Do đó, tam giác HEB đồng dạng với tam giác HDC (g.g)
Nên: \(\widehat {EBD} = \widehat {DCE}\) (2 góc tương ứng)
Xét tam giác AMB và tam giác ANC có:
\(\widehat {ABM} = \widehat {ACN}\)
\(\frac{{AB}}{{AC}} = \frac{{MB}}{{NC}}\)
Tam giác AMB đồng dạng với tam giác ANC (c.g.c)
\( \Rightarrow \widehat {BAM} = \widehat {CAN}\)
Do đó, hai góc BAC và góc MAN có cùng tia phân giác.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
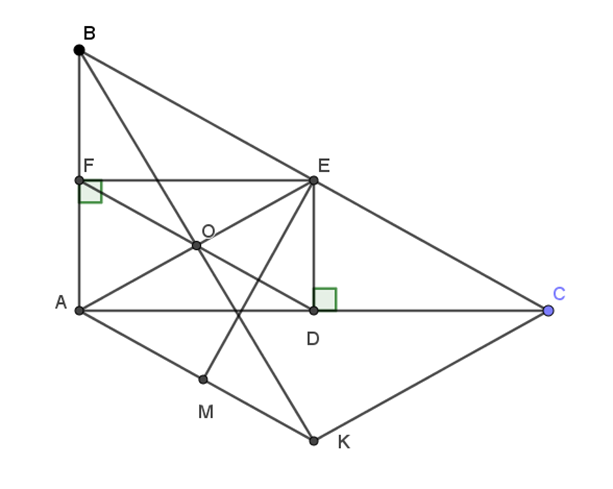
a)
EF vuông góc với AB do đó \(\widehat {AFE} = 90^\circ \)
ED vuông góc với AC do đó \(\widehat {ADE} = 90^\circ \)
Tứ giác ADEF có:
\(\widehat {FAD} = 90^\circ \)
\(\widehat {AFE} = 90^\circ \)
\(\widehat {ADE} = 90^\circ \)
Do đó, ADEF là hình chữ nhật
b)
K đối xứng với E qua D
Do đó D là trung điểm của EK
ED vuông góc với AC, AB vuông góc với AC
Do đó, ED song song với AB
Tam giác ABC có:
E là trung điểm của BC
ED song song với AB
Do đó, D là trung điểm của AC
Tứ giác AECK có:
D là trung điểm của AC, EK
Do đó, AECK là hình bình hành mà EK vuông góc với AC
Do đó, AECK là hình thoi
c)
ADEF là hình chữ nhật, DF và AE giao nhau tại O
Nên O là trung điểm của DF, AE và DF = AE
AECK là hình thoi nên AK = EC, AK song song với EC
AK = EC, BE = EC nên AK = BE
Tứ giác ABEK có:
AK = BE
AK song song với BE
Do đó, ABEK là hình bình hành
Do đó, AE, BK cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm của AE, O là trung điểm của BK
Do đó, B, O, K thẳng hàng
d)
Tam giác AME vuông tại M có MO là đường trung tuyến
\(MO = \frac{1}{2}AE = \frac{1}{2}DF\)
Tam giác FMD có:
\(MO = \frac{1}{2}DF\)
MO là đường trung tuyến
Do đó, FMD vuông tại M
\( \Rightarrow \widehat {DMF} = 90^\circ \)
Lời giải
\(\sin A = \cos B + \cos C = 2cos\frac{{B + C}}{2}.cos\frac{{B - C}}{2}\)
\( = 2\sin \frac{A}{2}.cos\frac{{B - C}}{2}\)
\( \Leftrightarrow 2\sin \frac{A}{2}.cos\frac{A}{2} = 2\sin \frac{A}{2}.cos\frac{{B - C}}{2}\)
\( \Leftrightarrow cos\frac{A}{2} = cos\frac{{B - C}}{2} \Rightarrow \frac{A}{2} = \frac{{B - C}}{2}\)
\(\begin{array}{l} \Rightarrow \widehat B = \widehat A + \widehat C\\ \Rightarrow 2\widehat B = 180^\circ \Rightarrow \widehat B = 90^\circ \end{array}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận