Cho hai hàm số y = −x + 3 và y = 3x − 1 có đồ thị lần lượt là hai đường thẳng d1 và d2.
a) Vẽ d1 và d2 trên cùng một hệ trục tọa độ.
b) Tính góc tạo bởi d1, d2 và trục Ox (làm tròn đến độ).
d) Tính khoảng cách từ O đến d1, d2.
Cho hai hàm số y = −x + 3 và y = 3x − 1 có đồ thị lần lượt là hai đường thẳng d1 và d2.
a) Vẽ d1 và d2 trên cùng một hệ trục tọa độ.
b) Tính góc tạo bởi d1, d2 và trục Ox (làm tròn đến độ).
d) Tính khoảng cách từ O đến d1, d2.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
a) +) Lấy hai điểm thuộc d1.
• x = 1 Þ y = 2 nên ta có điểm A(1; 2).
• x = 2 Þ y = 1 nên ta có điểm B(2; 1).
+) Lấy hai điểm thuộc d2.
• x = 1 Þ y = 2 nên ta có điểm A(1; 2).
• x = 0 Þ y = −1 nên ta có điểm C(0; −1).
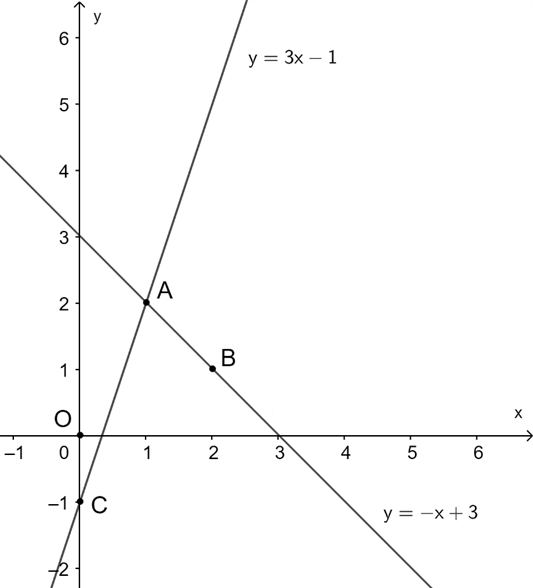
b) Tọa độ giao điểm là nghiệm của hệ phương trình
\[\left\{ \begin{array}{l}y = - x + 3\\y = 3x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\\3x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right. \Rightarrow A\left( {1;\;2} \right)\]
c) Ta có: \[\tan {\alpha _1} = {a_1} = - 1 \Rightarrow - {\alpha _1} = 45^\circ \].
Và \(\tan {\alpha _2} = {a_2} = 3 \Rightarrow {\alpha _2} \approx 71,565^\circ \).
Vậy \[\alpha = 180^\circ - 45^\circ - 71,565^\circ \approx 63^\circ \].
d) Khoảng cách từ O đến d1 là:
\({d_{O/{d_1}}} = \frac{{\left| 3 \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{1}{{\sqrt 2 }}\).
Khoảng cách từ O đến d2 là:
\({d_{O/{d_2}}} = \frac{{\left| { - 1} \right|}}{{\sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} = \frac{1}{{\sqrt {10} }}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
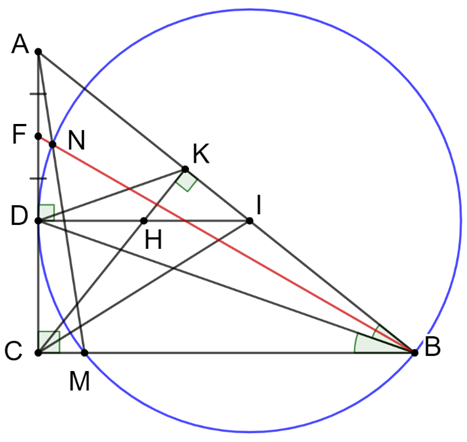
a) Ta có :
DI vuông CD (gt) Þ \(\widehat {IDC} = 90^\circ \)
CK vuông KI (gt) Þ \(\widehat {IKC} = 90^\circ \)
\( \Rightarrow \widehat {IDC} = \widehat {IKC} = 90^\circ \)
Mà 2 góc này ở 2 đỉnh kề nhau cùng nhìn cạnh CI
Suy ra CDIK là tứ giác nội tiếp.
b) Ta có:
\(\widehat {HCD} = \widehat {ABC}\) (cùng phụ góc \(\widehat {KCB}\))
Xét ∆HCD và ∆ABC có:
\(\widehat {HCD} = \widehat {ABC}\) (cmt )
\(\widehat {HDC} = \widehat {ACB} = 90^\circ \)
Suy ra ∆ABC ᔕ ∆HCD (g.g)
\( \Rightarrow \frac{{BC}}{{DC}} = \frac{{AC}}{{HD}}\) (2 cạnh tương ứng tỉ lệ )
Mà BD là đường phân giác của \(\widehat {ABC}\) (gt)
\( \Rightarrow \frac{{AB}}{{AD}} = \frac{{AC}}{{HD}}\)
Suy ra AD.AC = DH.AB (đpcm)
c) Gọi giao điểm của BN với AD là F'.
Ta có: AC là tiếp tuyến của (I;ID) nên \(\widehat {CDM} = \widehat {CBD} = \widehat {ABD}\)
\( \Rightarrow \widehat {MDB} = \widehat {CDB} - \widehat {CDM} = \widehat {CDB} - \widehat {ABD} = \widehat {CAB}\)
Mà \(\widehat {MDB} = \widehat {MNB} = \widehat {ANF'} \Rightarrow \widehat {ANF'} = \widehat {CAB}\)
Từ đó ∆F'AN ᔕ ∆F'BA (g.g)
\( \Rightarrow \frac{{F'A}}{{F'N}} = \frac{{F'B}}{{F'A}} \Rightarrow F'{A^2} = F'B\,.\,F'N\)
Mặt khác, vì F'D là tiếp tuyến của (I, ID) nên F'D2 = F'B.F'N
Þ F'A = F'D Þ F' ≡ F.
Từ đó ta có đpcm.
Lời giải
a) Hàm số \(y = \frac{1}{2}{x^2}\).
Bảng giá trị:
|
x |
– 2 |
– 1 |
0 |
1 |
2 |
|
y |
2 |
\(\frac{1}{2}\) |
0 |
\(\frac{1}{2}\) |
2 |
Đồ thị (P) của hàm số \(y = \frac{1}{2}{x^2}\)
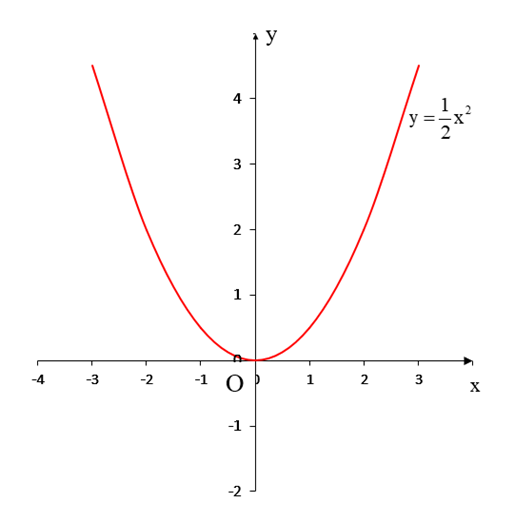
b) Điểm cách đều hai trục tọa độ nằm trên đường thẳng: y = x hoặc y = – x.
Xét phương trình hoành độ giao điểm của parabol (P)\(y = \frac{1}{2}{x^2}\) và đường thẳng y = x:
\(\frac{1}{2}{x^2} = x\)⟺ x2 – 2x = 0 ⇔ x(x – 2) = 0 \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
• Với x = 0 ⇒ y = 0 ⇒ điểm O (0; 0)
• Với x = 2 ⇒ y = 2 ⇒ điểm A (2; 2)
Xét phương trình hoành độ giao điểm của parabol (P)\(y = \frac{1}{2}{x^2}\) và đường thẳng y = − x:
\(\frac{1}{2}{x^2} = - x\)⟺ x2 + 2x = 0 ⇔ x(x + 2) = 0 \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = - 2}\end{array}} \right.\)
Với x = 0 ⇒ y = 0 ⇒ điểm O (0; 0)
Với x = −2 ⇒ y = 2 ⇒ điểm B (−2; 2)
Vậy có hai đểm A (2; 2) và B (−2; 2) trên (P) cách đều hai trục tọa độ.
c) Gọi điểm\(M\left( {{x_0};\,\,\frac{9}{2}} \right)\)∈ (P)
\( \Rightarrow \frac{9}{2} = \frac{1}{2}{\left( {{x_0}} \right)^2} \Leftrightarrow {\left( {{x_0}} \right)^2} = 9\)\[ \Leftrightarrow {x_0} = \left| 3 \right| \Rightarrow {x_0} = \pm 3\] ;
Vậy \({M_1}\left( {3;\,\,\frac{9}{2}} \right)\); \({M_2}\left( { - 3;\,\,\frac{9}{2}} \right) \in \left( P \right)\) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.