Câu hỏi:

19/08/2025 5,419

Cho đường thẳng (d) có phương trình y = (3m – 2)x + m – 2 (với m là tham số)
a) Tìm giá trị của m biết đường thẳng (d) đi qua điểm A(1; 2). Vẽ đồ thị hàm số với m tìm được

b) Đường thẳng (d) cắt Ox tại A, Oy tại B. Tìm m để diện tích ∆OAB bằng \(\frac{1}{2}\).

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Đường thẳng (d) đi qua điểm A(1; 2) nên suy ra

2 = (3m – 2) + m – 2

Û 4m − 6 = 0

\( \Leftrightarrow m = \frac{3}{2}\)

Vậy với \(m = \frac{3}{2}\) ta có đường thẳng \(\left( d \right):\;y = \frac{9}{2}x - \frac{1}{2}\)

+) Với x = 0 Þ \(y = - \frac{1}{2}\)

+) Với \(x = \frac{1}{2} \Rightarrow y = \frac{7}{4}\)

Ta có đồ thị hàm số của đường thẳng \(\left( d \right):\;y = \frac{9}{2}x - \frac{1}{2}\)

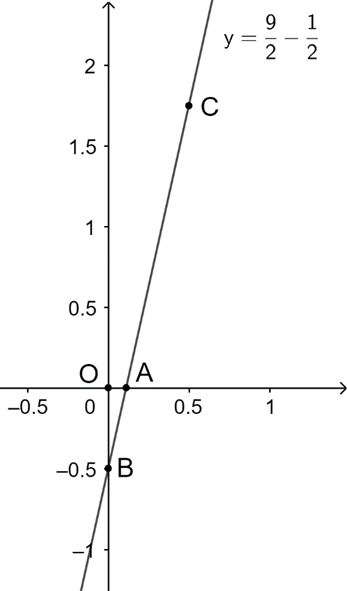
Cho đường thẳng (d) có phương trình y = (3m -2)x + m - 2 (với m là tham số) (ảnh 1)

b) Đường thẳng (d) cắt Ox tại \(A\left( {\frac{{2 - m}}{{3m - 2}};\;0} \right)\), Oy tại \(B\left( {0;\;m - 2} \right)\)

Khi đó diện tích tam giác OAB là:

\({S_{OAB}} = \frac{1}{2}OA\,.\,OB = \frac{1}{2}\,.\,\left| {\frac{{2 - m}}{{3m - 2}}} \right|\,.\,\left| {m - 2} \right|\)

Theo bài ra ta có:

\(\frac{1}{2}\,.\,\left| {\frac{{2 - m}}{{3m - 2}}} \right|\,.\,\left| {m - 2} \right| = \frac{1}{2}\)

\( \Leftrightarrow \left| {\frac{{2 - m}}{{3m - 2}}} \right|\,.\,\left| {m - 2} \right| = 1\)

\( \Leftrightarrow {\left( {m - 2} \right)^2} = \left| {3m - 2} \right|\)

\( \Rightarrow \left[ \begin{array}{l}{m^2} - 4m + 4 = 3m - 2\\{m^2} - 4m + 4 = 2 - 3m\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}{m^2} - 7m + 6 = 0\\{m^2} - m + 2 = 0\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m = 6\end{array} \right.\\VN\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 6\end{array} \right.\)

Vậy m = 1 và m = 6 là các giá trị của m thỏa mãn.

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại C (AC < BC), đường cao CK và đường phân giác trong BD (K Î AB, D Î AC). Qua D kẻ đường thẳng vuông góc với AC cắt CK, AB lần lượt tại H và I.

a) Chứng minh CDKI là tứ giác nội tiếp.

b) Chứng minh AD.AC = DH.AB

c) Gọi F là trung điểm AD. Đường tròn tâm I bán kính ID cắt BC tại M (M khác B) và cắt AM tại N (N khác M). Chứng minh B, N, F thẳng hàng.

Xem đáp án

Lời giải

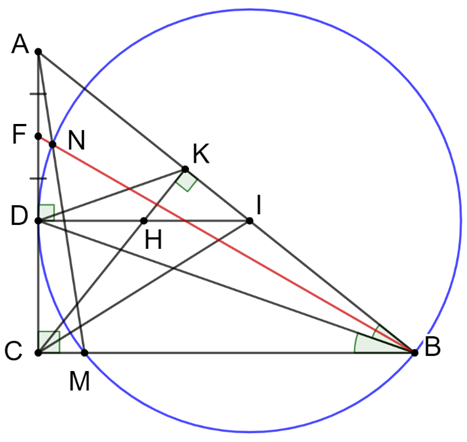
Cho tam giác ABC vuông tại C (AC < BC), đường cao CK và đường phân giác (ảnh 1)

a) Ta có :

DI vuông CD (gt) Þ \(\widehat {IDC} = 90^\circ \)

CK vuông KI (gt) Þ \(\widehat {IKC} = 90^\circ \)

\( \Rightarrow \widehat {IDC} = \widehat {IKC} = 90^\circ \)

Mà 2 góc này ở 2 đỉnh kề nhau cùng nhìn cạnh CI

Suy ra CDIK là tứ giác nội tiếp.

b) Ta có:

\(\widehat {HCD} = \widehat {ABC}\) (cùng phụ góc \(\widehat {KCB}\))

Xét ∆HCD và ∆ABC có:

\(\widehat {HCD} = \widehat {ABC}\) (cmt )

\(\widehat {HDC} = \widehat {ACB} = 90^\circ \)

Suy ra ∆ABC ᔕ ∆HCD (g.g)

\( \Rightarrow \frac{{BC}}{{DC}} = \frac{{AC}}{{HD}}\) (2 cạnh tương ứng tỉ lệ )

Mà BD là đường phân giác của \(\widehat {ABC}\) (gt)

\( \Rightarrow \frac{{AB}}{{AD}} = \frac{{AC}}{{HD}}\)

Suy ra AD.AC = DH.AB (đpcm)

c) Gọi giao điểm của BN với AD là F'.

Ta có: AC là tiếp tuyến của (I;ID) nên \(\widehat {CDM} = \widehat {CBD} = \widehat {ABD}\)

\( \Rightarrow \widehat {MDB} = \widehat {CDB} - \widehat {CDM} = \widehat {CDB} - \widehat {ABD} = \widehat {CAB}\)

Mà \(\widehat {MDB} = \widehat {MNB} = \widehat {ANF'} \Rightarrow \widehat {ANF'} = \widehat {CAB}\)

Từ đó ∆F'AN ᔕ ∆F'BA (g.g)

\( \Rightarrow \frac{{F'A}}{{F'N}} = \frac{{F'B}}{{F'A}} \Rightarrow F'{A^2} = F'B\,.\,F'N\)

Mặt khác, vì F'D là tiếp tuyến của (I, ID) nên F'D² = F'B.F'N

Þ F'A = F'D Þ F' ≡ F.

Từ đó ta có đpcm.

Câu 2

Cho hàm số \(y = \frac{1}{2}{x^2}\).

a) Vẽ đồ thị (P) của hàm số.

b) Tìm trên (P) những điểm cách đều hai trục tọa độ (không trùng với O).

c) Tìm trên (P) những điểm có tung độ bằng \(\frac{9}{2}\).

Xem đáp án

Lời giải

a) Hàm số \(y = \frac{1}{2}{x^2}\).

Bảng giá trị:

x	– 2	– 1	0	1	2
y	2	\(\frac{1}{2}\)	0	\(\frac{1}{2}\)	2

Đồ thị (P) của hàm số \(y = \frac{1}{2}{x^2}\)

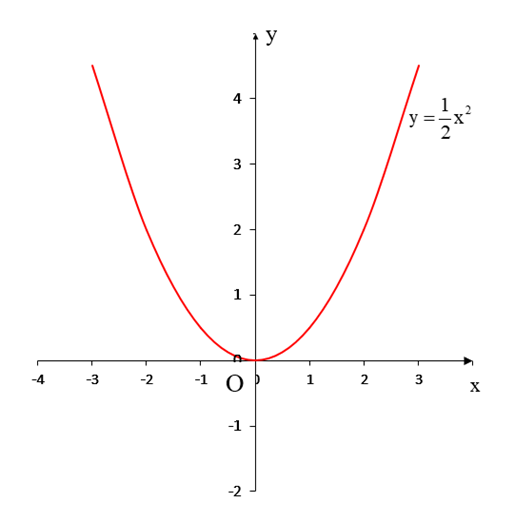
Cho hàm số y = 1/2x^2 a) vẽ đồ thị (P) của hàm số. b) Tìm trên (P) những điểm (ảnh 1)

b) Điểm cách đều hai trục tọa độ nằm trên đường thẳng: y = x hoặc y = – x.

Xét phương trình hoành độ giao điểm của parabol (P)\(y = \frac{1}{2}{x^2}\) và đường thẳng y = x:

\(\frac{1}{2}{x^2} = x\)⟺ x² – 2x = 0 ⇔ x(x – 2) = 0 \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)

• Với x = 0 ⇒ y = 0 ⇒ điểm O (0; 0)

• Với x = 2 ⇒ y = 2 ⇒ điểm A (2; 2)

Xét phương trình hoành độ giao điểm của parabol (P)\(y = \frac{1}{2}{x^2}\) và đường thẳng y = − x:

\(\frac{1}{2}{x^2} = - x\)⟺ x² + 2x = 0 ⇔ x(x + 2) = 0 \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = - 2}\end{array}} \right.\)

Với x = 0 ⇒ y = 0 ⇒ điểm O (0; 0)

Với x = −2 ⇒ y = 2 ⇒ điểm B (−2; 2)

Vậy có hai đểm A (2; 2) và B (−2; 2) trên (P) cách đều hai trục tọa độ.

c) Gọi điểm\(M\left( {{x_0};\,\,\frac{9}{2}} \right)\)∈ (P)

\( \Rightarrow \frac{9}{2} = \frac{1}{2}{\left( {{x_0}} \right)^2} \Leftrightarrow {\left( {{x_0}} \right)^2} = 9\)\[ \Leftrightarrow {x_0} = \left| 3 \right| \Rightarrow {x_0} = \pm 3\] ;

Vậy \({M_1}\left( {3;\,\,\frac{9}{2}} \right)\); \({M_2}\left( { - 3;\,\,\frac{9}{2}} \right) \in \left( P \right)\) .

Câu 3