Câu hỏi:
12/07/2024 915Câu hỏi trong đề: Chuyên đề Tin Học 11 KNTT Bài 4. Tháp Hà Nội có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Di chuyển 3 đĩa từ cọc 1 sang cọc 3:
1.1 Di chuyển 2 đĩa từ cọc 1 sang cọc 2:
- Di chuyển 1 đĩa từ cọc 1 sang cọc 3.
- Di chuyển 1 đĩa từ cọc 1 sang cọc 2.
- Di chuyển 1 đĩa từ cọc 3 sang cọc 2.
1.2. Di chuyển 1 đĩa từ cọc 1 sang cọc 3.
1.3. Di chuyển 2 đĩa từ cọc 2 sang cọc 3:
- Di chuyển 1 đĩa từ cọc 2 sang cọc 1.
- Di chuyển 1 đĩa từ cọc 2 sang cọc 3
- Di chuyển 1 đĩa từ cọc 1 sang cọc 3.
2. Di chuyển 1 đĩa từ cọc 1 sang cọc 2.
3. Di chuyển 3 đĩa từ cọc 3 sang cọc 2:
3.1 Di chuyển 2 đĩa từ cọc 3 sang cọc 1:
- Di chuyển 1 đĩa từ cọc 3 sang cọc 2. 3.1.2
- Di chuyển 1 đĩa từ cọc 3 sang cọc 1.
- Di chuyển 1 đĩa từ cọc 2 sang cọc 1.
3.2 Di chuyển 1 đĩa từ cọc 3 sang cọc 2.
3.3 Di chuyển 2 đĩa từ cọc 1 sang cọc 2:
- Di chuyển 1 đĩa từ cọc 1 sang cọc 3.
- Di chuyển 1 đĩa từ cọc 1 sang cọc 2.
- Di chuyển 1 đĩa từ cọc 3 sang cọc 2.
Vậy, tổng số bước để di chuyển 4 đĩa theo quy trình trên là:
- Di chuyển 3 đĩa từ cọc 1 sang cọc 2: 7 bước
- Di chuyển đĩa còn lại từ cọc 1 sang cọc 3: 1 bước
- Di chuyển 3 đĩa từ cọc 2 sang cọc 3: 7 bước
Vậy tổng số bước cần thiết để di chuyển 4 đĩa trong bài toán tháp Hà Nội là 15 bước.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
- Nếu chỉ có một đĩa (n=1), H(n) = 1.
- Nếu có n đĩa, để chuyển tất cả các đĩa từ tháp ban đầu sang tháp đích, ta phải thực hiện các bước sau:
Chuyển n-1 đĩa từ tháp ban đầu sang tháp trung gian.
Chuyển đĩa cuối cùng (đĩa lớn nhất) từ tháp ban đầu sang tháp đích.
Chuyển n-1 đĩa từ tháp trung gian sang tháp đích.
Số bước chuyển tất cả các đĩa là H(n) = 2 * H(n-1) + 1.
- Ta sẽ chứng minh công thức này bằng phương pháp quy nạp toán học:
Bước 1: Giả sử công thức đúng với n-1, tức là H(n-1) = 2^(n-1) - 1
Bước 2: Chứng minh công thức đúng với n, tức là H(n) = 2^n - 1
Ta có:
H(n) = 2 * H(n-1) + 1 (theo công thức đề bài)
= 2 * (2^(n-1) - 1) + 1 (theo giả sử ở bước 1)
= 2^n - 2 + 1
= 2^n - 1
Vậy ta đã chứng minh được công thức đúng với mọi n.
Để tính H(64), ta áp dụng công thức đã chứng minh:
H(64) = 2^64 - 1
= 18446744073709551615
Vậy H(64) = 18446744073709551615 trùng với con số ở trên bài báo
Lời giải
* Với n = 1, bài toán trở nên rất đơn giản, chỉ cần chuyển đĩa từ cột xuất phát sang cột đích là xong
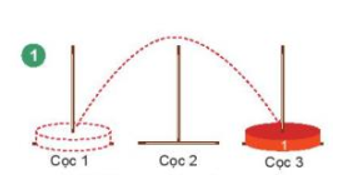
* Với n = 2, ta sẽ thực hiện theo các bước sau:
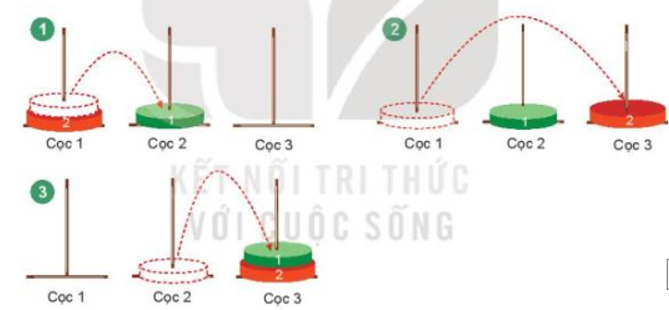
* Với n = 3, ta sẽ thực hiện theo các bước sau:
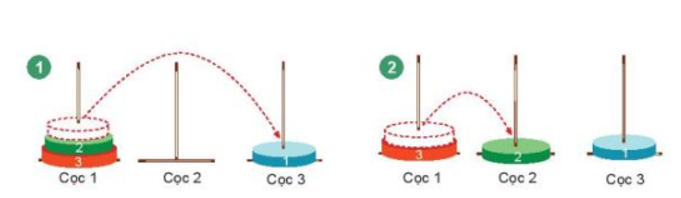
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 1)
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 25 có đáp án
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 2)
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 26 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 27 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 28 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 1: Một số thao tác chỉnh sửa ảnh và hỗ trợ chỉnh sửa ảnh có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 24 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận