Câu hỏi:
12/07/2024 595
Hãy chứng minh công thức bằng quy nạp toán học. Hãy tính H(64) và so sánh với con số các bước đã được đưa ra trong tờ quảng cáo của trò chơi vào năm 1883.
Hãy chứng minh công thức bằng quy nạp toán học. Hãy tính H(64) và so sánh với con số các bước đã được đưa ra trong tờ quảng cáo của trò chơi vào năm 1883.
Câu hỏi trong đề: Chuyên đề Tin Học 11 KNTT Bài 4. Tháp Hà Nội có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
- Nếu chỉ có một đĩa (n=1), H(n) = 1.
- Nếu có n đĩa, để chuyển tất cả các đĩa từ tháp ban đầu sang tháp đích, ta phải thực hiện các bước sau:
Chuyển n-1 đĩa từ tháp ban đầu sang tháp trung gian.
Chuyển đĩa cuối cùng (đĩa lớn nhất) từ tháp ban đầu sang tháp đích.
Chuyển n-1 đĩa từ tháp trung gian sang tháp đích.
Số bước chuyển tất cả các đĩa là H(n) = 2 * H(n-1) + 1.
- Ta sẽ chứng minh công thức này bằng phương pháp quy nạp toán học:
Bước 1: Giả sử công thức đúng với n-1, tức là H(n-1) = 2^(n-1) - 1
Bước 2: Chứng minh công thức đúng với n, tức là H(n) = 2^n - 1
Ta có:
H(n) = 2 * H(n-1) + 1 (theo công thức đề bài)
= 2 * (2^(n-1) - 1) + 1 (theo giả sử ở bước 1)
= 2^n - 2 + 1
= 2^n - 1
Vậy ta đã chứng minh được công thức đúng với mọi n.
Để tính H(64), ta áp dụng công thức đã chứng minh:
H(64) = 2^64 - 1
= 18446744073709551615
Vậy H(64) = 18446744073709551615 trùng với con số ở trên bài báo
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1. Di chuyển 3 đĩa từ cọc 1 sang cọc 3:
1.1 Di chuyển 2 đĩa từ cọc 1 sang cọc 2:
- Di chuyển 1 đĩa từ cọc 1 sang cọc 3.
- Di chuyển 1 đĩa từ cọc 1 sang cọc 2.
- Di chuyển 1 đĩa từ cọc 3 sang cọc 2.
1.2. Di chuyển 1 đĩa từ cọc 1 sang cọc 3.
1.3. Di chuyển 2 đĩa từ cọc 2 sang cọc 3:
- Di chuyển 1 đĩa từ cọc 2 sang cọc 1.
- Di chuyển 1 đĩa từ cọc 2 sang cọc 3
- Di chuyển 1 đĩa từ cọc 1 sang cọc 3.
2. Di chuyển 1 đĩa từ cọc 1 sang cọc 2.
3. Di chuyển 3 đĩa từ cọc 3 sang cọc 2:
3.1 Di chuyển 2 đĩa từ cọc 3 sang cọc 1:
- Di chuyển 1 đĩa từ cọc 3 sang cọc 2. 3.1.2
- Di chuyển 1 đĩa từ cọc 3 sang cọc 1.
- Di chuyển 1 đĩa từ cọc 2 sang cọc 1.
3.2 Di chuyển 1 đĩa từ cọc 3 sang cọc 2.
3.3 Di chuyển 2 đĩa từ cọc 1 sang cọc 2:
- Di chuyển 1 đĩa từ cọc 1 sang cọc 3.
- Di chuyển 1 đĩa từ cọc 1 sang cọc 2.
- Di chuyển 1 đĩa từ cọc 3 sang cọc 2.
Vậy, tổng số bước để di chuyển 4 đĩa theo quy trình trên là:
- Di chuyển 3 đĩa từ cọc 1 sang cọc 2: 7 bước
- Di chuyển đĩa còn lại từ cọc 1 sang cọc 3: 1 bước
- Di chuyển 3 đĩa từ cọc 2 sang cọc 3: 7 bước
Vậy tổng số bước cần thiết để di chuyển 4 đĩa trong bài toán tháp Hà Nội là 15 bước.
Lời giải
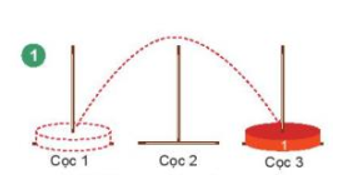
* Với n = 1, bài toán trở nên rất đơn giản, chỉ cần chuyển đĩa từ cột xuất phát sang cột đích là xong
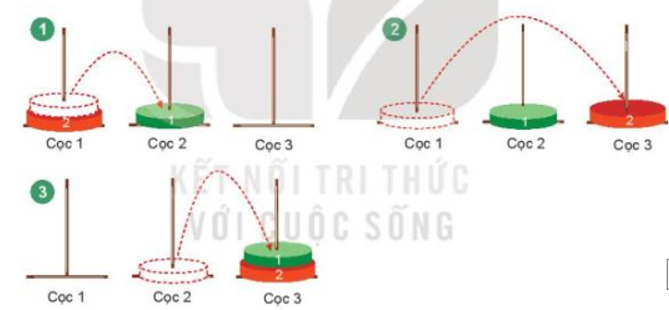
* Với n = 2, ta sẽ thực hiện theo các bước sau:
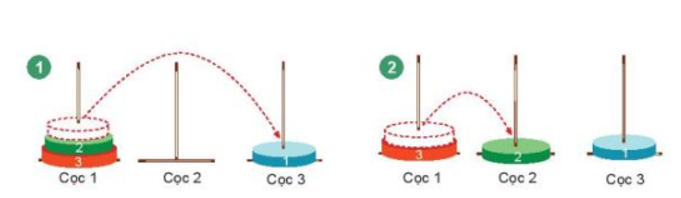
* Với n = 3, ta sẽ thực hiện theo các bước sau:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 2)
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 26 có đáp án
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 1)
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 1: Một số thao tác chỉnh sửa ảnh và hỗ trợ chỉnh sửa ảnh có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 25 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 28 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 27 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 2: Tẩy xóa ảnh có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận