Câu hỏi:

12/07/2024 865

Cho 2 hàm số bậc nhất: y = mx + 3 và y = (2m + 1)x – 5. Tìm giá trị m để đồ thị của hai hàm số đã cho là:

a) hai đường thẳng song song.

b) hai đường thẳng cắt nhau.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

Điều kiện để hai hàm số là hàm số bậc nhất: m ≠ 0, \(m \ne \frac{{ - 1}}{2}\).

a) Hai đường thẳng đã cho là hai đường thẳng song song

\( \Leftrightarrow \left\{ \begin{array}{l}m = 2m + 1\\3 \ne - 5\end{array} \right. \Leftrightarrow m = - 1\) (thỏa mãn)

Vậy m = – 1.

b) Hai đường thẳng đã cho là hai đường thẳng cắt nhau

⇔ m ≠ 2m + 1

⇔ m ≠ – 1

Vậy m ≠ 0, \(m \ne \frac{{ - 1}}{2}\), m ≠ – 1.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.

a) Chứng minh tam giác COD vuông tại O.

b) Chứng minh AC . BD = R².

c) Kẻ MH vuông góc AB (H ∈ AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH.

Xem đáp án

Lời giải

Media VietJack

a) Xét (O) có CA, CM là hai tiếp tuyến cắt nhau tại C

Suy ra AC = CM và OC là tia phân giác của \(\widehat {AOM}\)

Do đó \(\widehat {AOC} = \widehat {COM} = \frac{1}{2}\widehat {AOM}\)

Xét (O) có DB, DM là hai tiếp tuyến cắt nhau tại D

Suy ra BD = DM và OD là tia phân giác của \(\widehat {BOM}\)

Do đó \(\widehat {BOD} = \widehat {DOM} = \frac{1}{2}\widehat {BOM}\)

Ta có \(\widehat {COD} = \widehat {COM} + \widehat {DOM} = \frac{1}{2}\widehat {AOM} + \frac{1}{2}\widehat {BOM} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.180^\circ = 90^\circ \)

Vậy tam giác COD vuông tại O.

b) Xét tam giác COD vuông tại O có OM ⊥ CD, theo hệ thức lượng trong tam giác vuông ta có: OM² = CM . DM

Mà CM = AC, DM = BD (chứng minh câu a)

Suy ra AC . BD = R².

c) Gọi I là giao điểm của MH và BC, K là giao điểm của MB và AC

Xét (O) có DB, DM là hai tiếp tuyến cắt nhau tại O, suy ra BM ⊥ DO

Mà OC ⊥ DO (chứng minh câu a)

Do đó OC // BM (quan hệ từ vuông góc đến song song)

Xét tam giác ABK có

O là trung điểm của AB; OC // BM

Suy ra C là trung điểm của AK

Do đó CA = CK

Ta có CA ⊥ AB, MH ⊥ AB nên CA // MH (quan hệ từ vuông góc đến song song)

Suy ra \(\frac{{MI}}{{CK}} = \frac{{BI}}{{BC}} = \frac{{IH}}{{AC}}\)

Mà CA = CK, suy ra MI = IH

Do đó I là trung điểm của MH

Vậy BC đi qua trung điểm của đoạn MH.

Câu 2

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Tìm giao điểm Q của SD và (MNP).

Xem đáp án

Lời giải

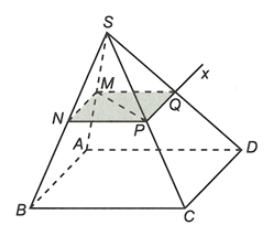
Media VietJack

Xét tam giác SAB có M, N là trung điểm SA, SB

Suy ra MN là đường trung bình

Do đó MN // AB

Mà AB // DC (vì ABCD là hình bình hành)

Suy ra MN // CD

Xét (MNP) và (SDC) có P là điểm chung và MN // CD (chứng minh trên)

Suy ra giao tuyến qua P song song với MN, giao với SD tại Q

Do đó SD ∩ (MNP) = PQ.

Câu 3