Cho nửa đường tròn (O; R) đường kính AB. Trên đoạn OB lấy điểm H sao cho HB = 2HO. Đường thẳng vuông góc với AB tại H cắt nửa (O) tại D. Vẽ đường tròn (S) đường kính AO cắt AD tại C.
a) Chứng minh C là trung điểm của AD.
b) Chứng minh 4 điểm C, D, H, O cùng thuộc một đường tròn.
c) CB cắt DO tại E. Chứng minh BC là tiếp tuyến của (S).
d) Tính diện tích tam giác AEB theo R.
Cho nửa đường tròn (O; R) đường kính AB. Trên đoạn OB lấy điểm H sao cho HB = 2HO. Đường thẳng vuông góc với AB tại H cắt nửa (O) tại D. Vẽ đường tròn (S) đường kính AO cắt AD tại C.
a) Chứng minh C là trung điểm của AD.
b) Chứng minh 4 điểm C, D, H, O cùng thuộc một đường tròn.
c) CB cắt DO tại E. Chứng minh BC là tiếp tuyến của (S).
d) Tính diện tích tam giác AEB theo R.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
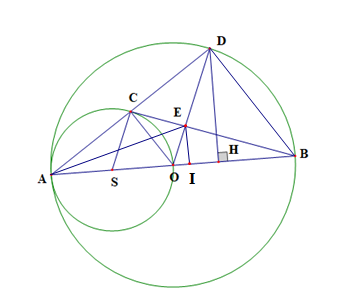
a) Vì tam giác ACO nội tiếp (S) đường kính AO nên tam giác ACO vuông tại C
Suy ra AC ⊥ CO
Xét (O) có AD là dây cung, AD ⊥ CO
Suy ra C là trung điểm của AD.
b) Xét tứ giác COHD có: \(\widehat {DCO} + \widehat {DHO} = 90^\circ + 90^\circ = 180^\circ \)
Þ tứ giác COHD nội tiếp
Vậy 4 điểm C, D, H, O cùng thuộc một đường tròn.
c) Ta có BH = 2HO, BH + HO = BO = R
\( \Rightarrow BH = \frac{2}{3}R,OH = \frac{1}{3}R\)
Ta có \(AH = AB - BH = 2{\rm{R}} - \frac{2}{3}R = \frac{4}{3}R\)
Þ AH = 2HB
Vì tam giác ABD nội tiếp (O) đường kính AB nên tam giác ABD vuông tại D
Mà BH ⊥ AB
Þ AD2 = AH . AB và BD2 = BH . AB
Þ AH = 2HB
Þ AD2 = 2BD2
\( \Rightarrow B{{\rm{D}}^2} = \frac{{A{{\rm{D}}^2}}}{2} = \frac{{A{\rm{D}}.2C{\rm{D}}}}{2} = A{\rm{D}}.C{\rm{D}}\)
\( \Rightarrow \frac{{B{\rm{D}}}}{{A{\rm{D}}}} = \frac{{C{\rm{D}}}}{{B{\rm{D}}}}\)
Xét tam giác DBC và tam giác DAB có
\(\frac{{B{\rm{D}}}}{{A{\rm{D}}}} = \frac{{C{\rm{D}}}}{{B{\rm{D}}}}\) (chứng minh trên);
\(\widehat {A{\rm{D}}B}\) là góc chung
(c.g.c)
\( \Rightarrow \widehat {{\rm{D}}BC} = \widehat {DAB}\) (hai góc tương ứng)
Ta có CO ⊥ AD, BD ⊥ AD
Nên CO // BD (quan hệ từ vuông góc đến song song)
\( \Rightarrow \widehat {{\rm{D}}BC} = \widehat {BCO}\) (hai góc so le trong)
Mà \(\widehat {{\rm{D}}BC} = \widehat {DAB}\) (chứng minh trên)
\( \Rightarrow \widehat {{\rm{DA}}B} = \widehat {BCO}\)
Vì SC = SO nên tam giác SCO cân tại S \( \Rightarrow \widehat {SCO} = \widehat {SOC}\)
Vì tam giác ACO vuông tại C nên
\(\widehat {CAO} + \widehat {COA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {SCO} = \widehat {SOC}\), \(\widehat {{\rm{DA}}B} = \widehat {BCO}\)
\( \Rightarrow \widehat {BCO} + \widehat {SCO} = 90^\circ \), hay \(\widehat {BC{\rm{S}}} = 90^\circ \)
Do đó SC ⊥ CB
Xét (S) có SC ⊥ CB
Suy ra BC là tiếp tuyến của (S).
d) Xét tam giác SCO có \(\widehat {SCO} + \widehat {SOC} + \widehat {C{\rm{S}}O} = 180^\circ \) (tổng 3 góc trong một tam giác)
Mà \(\widehat {SCO} = \widehat {SOC}\)
\( \Rightarrow \widehat {C{\rm{S}}O} = 180^\circ - 2\widehat {SOC}\) (1)
Vì OB = OD nên tam giác OBD cân tại O
\( \Rightarrow \widehat {BDO} = \widehat {OB{\rm{D}}}\)
Xét tam giác BDO có \(\widehat {B{\rm{D}}O} + \widehat {BOD} + \widehat {OB{\rm{D}}} = 180^\circ \) (tổng 3 góc trong một tam giác)
Mà \(\widehat {BDO} = \widehat {OB{\rm{D}}}\)
\( \Rightarrow \widehat {BOD} = 180^\circ - 2\widehat {OB{\rm{D}}}\) (2)
Vì OC // BD nên \(\widehat {OB{\rm{D}}} = \widehat {SOC}\) (3)
Từ (1) , (2) và (3) ta có \(\widehat {BO{\rm{D}}} = \widehat {OSC}\)
Mà hai góc này ở vị trí đồng vị
Þ OD // SC
Mà SC ⊥ CB
Þ OD ⊥ CB (quan hệ từ vuông góc đến song song)
Xét tam giác BCD có DE ⊥ CB
Nên DE . CB = CD . BD
Suy ra \[DE = \frac{{C{\rm{D}}.B{\rm{D}}}}{{CB}}\]
Vì tam giác OHD vuông tại H nên theo định lý Pytago có
\[{\rm{D}}H = \sqrt {O{{\rm{D}}^2} - O{H^2}} = \sqrt {{R^2} - {{\left( {\frac{1}{3}R} \right)}^2}} = \frac{{\sqrt 8 R}}{3}\]
Vì tam giác BHD vuông tại H nên theo định lý Pytago có
\[{\rm{DB}} = \sqrt {{\rm{H}}{{\rm{D}}^2} + B{H^2}} = \sqrt {{{\left( {\frac{{\sqrt 8 R}}{3}} \right)}^2} + {{\left( {\frac{2}{3}R} \right)}^2}} = \frac{{\sqrt {12} R}}{3}\]
Vì tam giác ABD vuông tại D nên theo định lý Pytago có
\[{\rm{AD}} = \sqrt {A{B^2} - B{D^2}} = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {\frac{{\sqrt {12} }}{3}R} \right)}^2}} = \frac{{2\sqrt 6 R}}{3}\]
Suy ra \[{\rm{CD}} = \frac{1}{2}{\rm{AD}} = \frac{{\sqrt 6 R}}{3}\]
Vì tam giác BCD vuông tại D nên theo định lý Pytago có
\[{\rm{CB}} = \sqrt {{\rm{C}}{{\rm{D}}^2} + B{D^2}} = \sqrt {{{\left( {\frac{{\sqrt 6 R}}{3}} \right)}^2} + {{\left( {\frac{{\sqrt {12} }}{3}R} \right)}^2}} = \sqrt 2 R\]
Suy ra \[DE = \frac{{C{\rm{D}}.B{\rm{D}}}}{{CB}} = \frac{{\frac{{\sqrt 6 R}}{3}.\frac{{\sqrt {12} R}}{3}}}{{\sqrt 2 R}} = \frac{{2R}}{3}\]
Kẻ EI ⊥ AB
Mà DH ⊥ AB nên EI // DH
Suy ra \(\frac{{DH}}{{EI}} = \frac{{OD}}{{OE}}\)
Do đó \(\frac{{DH}}{{DH - EI}} = \frac{{OD}}{{O{\rm{D}} - OE}} = \frac{{OD}}{{E{\rm{D}}}}\)
Suy ra \(\frac{{\frac{{\sqrt 8 R}}{3}}}{{\frac{{\sqrt 8 R}}{3} - EI}} = \frac{R}{{\frac{{2R}}{3}}}\)
Do đó \[{\rm{EI = }}\frac{{\sqrt 8 R}}{9}\]
Ta có \[{{\rm{S}}_{A{\rm{E}}B}} = \frac{1}{2}EI.AB = \frac{1}{2}\frac{{\sqrt 8 R}}{9}.2{\rm{R = }}\frac{{\sqrt 8 {R^2}}}{9}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải

a) Xét (O) có CA, CM là hai tiếp tuyến cắt nhau tại C
Suy ra AC = CM và OC là tia phân giác của \(\widehat {AOM}\)
Do đó \(\widehat {AOC} = \widehat {COM} = \frac{1}{2}\widehat {AOM}\)
Xét (O) có DB, DM là hai tiếp tuyến cắt nhau tại D
Suy ra BD = DM và OD là tia phân giác của \(\widehat {BOM}\)
Do đó \(\widehat {BOD} = \widehat {DOM} = \frac{1}{2}\widehat {BOM}\)
Ta có \(\widehat {COD} = \widehat {COM} + \widehat {DOM} = \frac{1}{2}\widehat {AOM} + \frac{1}{2}\widehat {BOM} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.180^\circ = 90^\circ \)
Vậy tam giác COD vuông tại O.
b) Xét tam giác COD vuông tại O có OM ⊥ CD, theo hệ thức lượng trong tam giác vuông ta có: OM2 = CM . DM
Mà CM = AC, DM = BD (chứng minh câu a)
Suy ra AC . BD = R2.
c) Gọi I là giao điểm của MH và BC, K là giao điểm của MB và AC
Xét (O) có DB, DM là hai tiếp tuyến cắt nhau tại O, suy ra BM ⊥ DO
Mà OC ⊥ DO (chứng minh câu a)
Do đó OC // BM (quan hệ từ vuông góc đến song song)
Xét tam giác ABK có
O là trung điểm của AB; OC // BM
Suy ra C là trung điểm của AK
Do đó CA = CK
Ta có CA ⊥ AB, MH ⊥ AB nên CA // MH (quan hệ từ vuông góc đến song song)
Suy ra \(\frac{{MI}}{{CK}} = \frac{{BI}}{{BC}} = \frac{{IH}}{{AC}}\)
Mà CA = CK, suy ra MI = IH
Do đó I là trung điểm của MH
Vậy BC đi qua trung điểm của đoạn MH.
Lời giải
Lời giải
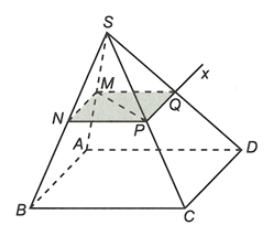
Xét tam giác SAB có M, N là trung điểm SA, SB
Suy ra MN là đường trung bình
Do đó MN // AB
Mà AB // DC (vì ABCD là hình bình hành)
Suy ra MN // CD
Xét (MNP) và (SDC) có P là điểm chung và MN // CD (chứng minh trên)
Suy ra giao tuyến qua P song song với MN, giao với SD tại Q
Do đó SD ∩ (MNP) = PQ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.