Câu hỏi:
15/05/2023 717
Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C ≠ A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB tại H, MB cắt (O) tại Q và cắt CH tại N.
a) Chứng minh MA2 = MQ.MB.
b) MO cắt AC tại I. Chứng minh tứ giác AIQM nội tiếp.
c) Chứng minh: IN ⊥ CH.
Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C ≠ A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB tại H, MB cắt (O) tại Q và cắt CH tại N.
a) Chứng minh MA2 = MQ.MB.
b) MO cắt AC tại I. Chứng minh tứ giác AIQM nội tiếp.
c) Chứng minh: IN ⊥ CH.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
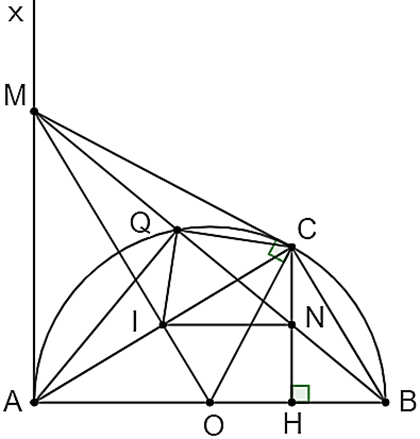
a) ∆AQB nội tiếp đường tròn (O)
\( \Rightarrow \widehat {AQB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
⇒ AQ ⊥ QB hay AQ ⊥ BM.
∆ABM vuông tại A (do Ax là tiếp tuyến của (O) nên Ax ⊥ AB) có AQ ⊥ BM, ta áp dụng hệ thức lượng trong tam giác vuông suy ra: MA2 = MQ . MB (đpcm).
b) ∆ACB nội tiếp đường tròn (O)
\( \Rightarrow \widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
⇒ AC ⊥ CB. (1)
Ta có: OA = OC (Bán kính của đường tròn tâm O)
Và MA = MC (Hai tiếp tuyến MA, MC cắt nhau tại M)
Suy ra MO là đường trung trực của đoạn thẳng AC.
⇒ MO ⊥ AC. (2)
Từ (1) và (2) suy ra BC // OM (cùng vuông góc với AC).
\( \Rightarrow \widehat {OMB} = \widehat {MBC}\) (so le trong).
Hay \(\widehat {IMQ} = \widehat {MBC}\). (3)
Mặt khác: \(\widehat {QAI} = \widehat {MBC}\) (Hai góc nội tiếp đường tròn (O) cùng chắn cung QC). (4)
Từ (3) và (4), suy ra \(\widehat {IMQ} = \widehat {QAI}\).
Do M và A cùng nhìn QI cố định dưới hai góc bằng nhau nên tứ giác AIQM nội tiếp.
c) Do tứ giác AIQM nội tiếp nên suy ra:
\(\widehat {AMI} = \widehat {AQI}\) (Hai góc nội tiếp đường tròn cùng chắn cung AI) (5)
Ta có: \(\widehat {IQN} = \widehat {AQB} - \widehat {AQI} = 90^\circ - \widehat {AQI}\) (6).
Xét tam giác AIM vuông tại I có \(\widehat {AMI} + \widehat {MAI} = 90^\circ \).
Và \(\widehat {MAI} + \widehat {IAO} = \widehat {MAO} = 90^\circ \).
Suy ra \(\widehat {AMI} = \widehat {IAO}\) (Hai góc cùng phụ với \(\widehat {MAI}\)) (7)
Xét tam giác CAH vuông tại H có:
\(\widehat {CAH} + \widehat {ACH} = 90^\circ \Rightarrow \widehat {ACH} = 90^\circ - \widehat {CAH}\)
Hay \(\widehat {ICN} = 90^\circ - \widehat {IAO}\) (8).
Từ (5), (6), (7) và (8), suy ra \(\widehat {IQN} = \widehat {ICN}\).
Do Q và C cùng nhìn IN cố định dưới hai góc bằng nhau nên tứ giác IQCN nội tiếp.
\( \Rightarrow \widehat {CIN} = \widehat {CQN}\) (Hai góc nội tiếp đường tròn cùng chắn cung CN) (*)
Mà \(\widehat {CAB} = \widehat {CQB}\) (Hai góc nội tiếp đường tròn (O) cùng chắn cung CB) (**)
Từ (*) và (**) suy ra \(\widehat {CIN} = \widehat {CAH}\).
Suy ra IN // AH (Có hai góc ở vị trí đồng vị bằng nhau)
Mà AH ⊥ CH nên suy ra IN ⊥ CH.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m, chiều rộng 5m, chiều sâu 3m.
a. Tính thể tích của hồ bơi.
b. Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).
c. Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.
Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m, chiều rộng 5m, chiều sâu 3m.
a. Tính thể tích của hồ bơi.
b. Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).
c. Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.
Xem đáp án »
12/07/2024
34,495
Câu 2:
Cho 2 tập hợp \(M = \left[ {2m - 1;2m + 5} \right]\) và \(N = \left[ {m + 1;m + 7} \right]\)(với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.
Xem đáp án »
15/05/2023
20,099
Câu 3:
Cho hình tròn tâm O, đường kính AB = 8 cm.
a. Tính chu vi hình tròn tâm O đường kính AB, hình tròn tâm M, đường kính AO và hình tròn tâm N, đường kính OB.
b. So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.
c. Tính diện tích phần đã tô đậm của hình tròn tâm O.
Cho hình tròn tâm O, đường kính AB = 8 cm.
a. Tính chu vi hình tròn tâm O đường kính AB, hình tròn tâm M, đường kính AO và hình tròn tâm N, đường kính OB.
b. So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.
c. Tính diện tích phần đã tô đậm của hình tròn tâm O.
Xem đáp án »
15/05/2023
7,386
Câu 4:
Hai đội công nhân cùng làm một đoạn đường trong 24 ngày thì xong. Mỗi ngày đội thứ hai làm được khối lượng công việc nhiều gấp đôi đội thứ nhất. Hỏi nếu làm một mình thì mỗi đội làm xong đoạn đường đó trong bao lâu?
Xem đáp án »
15/05/2023
6,171
Câu 5:
Các cột điện trước đây cách nhau 60 m, hiện nay trồng lại cách nhau 45 m. Hỏi sau cột đầu tiên không phải trồng lại thì cột gần nhất không phải trồng lại là cột thứ mấy?
Xem đáp án »
15/05/2023
5,843
Câu 6:
Cho 3 số dương x, y, z thỏa mãn điều kiện: xy + yz +zx = 1. Tính:
\(A = x\sqrt {\frac{{\left( {{y^2} + 1} \right)\left( {{z^2} + 1} \right)}}{{{x^2} + 1}}} + y\sqrt {\frac{{\left( {1 + {z^2}} \right)\left( {1 + {x^2}} \right)}}{{1 + {y^2}}}} + z\sqrt {\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{1 + {z^2}}}} \).
Cho 3 số dương x, y, z thỏa mãn điều kiện: xy + yz +zx = 1. Tính:
\(A = x\sqrt {\frac{{\left( {{y^2} + 1} \right)\left( {{z^2} + 1} \right)}}{{{x^2} + 1}}} + y\sqrt {\frac{{\left( {1 + {z^2}} \right)\left( {1 + {x^2}} \right)}}{{1 + {y^2}}}} + z\sqrt {\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{1 + {z^2}}}} \).
Xem đáp án »
15/05/2023
4,960
Câu 7:
Một ô tô cứ đi 100 km thì tiêu thụ hết 12,5 lít xăng. Hỏi ô tô đó đi quãng đường dài 60 km thì tiêu thụ hết bao nhiêu xăng?
Xem đáp án »
12/07/2024
4,244
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận